Adding one to the number represented as array of digits

Problem statement:

We are given an array of digits from 0 to 9, which represent a number. The first element of the array represents the most significant bit of the number, and the last element of the array represents the least significant number.

Since it is also given that the number would be a non-negative number, so there is no extra element required for the sign bit (since, by default, non-negative numbers don't require any extra bit for a sign).

We aim to add 1 to this number and store it in the array, or we can say we have to increment the number by one represented in the array.

For example: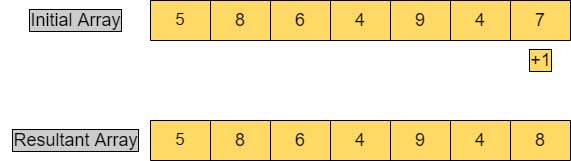

In the above example, the array represents the number 5864947, and we added one into this, so now the value is 5864948, which is represented in the form of an array.

Let's suppose we have n digits in the number initially so that it will be represented by n elements in the array. In the worst case, we will have n + 1 elements in the resultant array.

For example: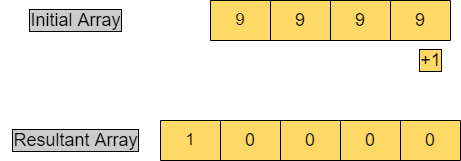

In the above example, we have four elements in the array which are representing the number 9999, and if we add 1, our number is equal to 10000, which is represented by five elements.

Method 1

The first way to approach this problem is that we will get the number in the form of an integer from the array. Then we will add 1 to the number, and the resulting integer is then converted into an array.

Java Code:

Output: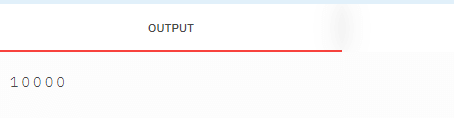

Explanation

In the above code, we have an array that represents the number, and we have two functions.

One function is returning the number equivalent of an array using the division method. Then after getting the equivalent number, we increment the number by 1. Now we convert this num into the array using the second function.

In the second function, firstly, we calculated the number of digits in our number and then declared the size of the array equal to the number of digits. Then we filled each digit in the array by division method.

So if n represents the number of elements in an array, then time complexity would be: O(n), and space complexity would also be: O(n).

Method 2

Instead of converting the array into the number and then again converting it into the array, we can directly operate on the array.

But here, the size of the resultant array can be increased by one, so we will use ArrayList instead of an array to adjust the size dynamically.

Java code:

Output:

Explanation

In the above code, we have an array that represents the number. We will use extra variables to maintain the carry. Initially, carry is zero, and we will use an ArrayList to store the resultant values.

We will start from the end of the array till the start because we will add elements from the least significant bit to the most significant bit.

Since we have to add one to the original number, we will add carry and one to the last element of the array. If that value is greater than 9, then we will convert the value by getting modulo with ten, and the carry bit will be 1. And for all other elements, we will add carry to that particular element and transfer carry to the next digits in the left-hand side.

In the end, if carry is one, then we will add 1 to the 0th index of the resultant ArrayList. Otherwise, we will not.

So, by this methodology, we will get the equivalent number in the ArrayList.

So the time complexity would be O(n), where n is the elements in the array.

Space complexity would be O(n) for storing the result in ArrayList.