Maximum Sum Rectangle in a 2D Matrix

Problem Statement: Given a 2D matrix of integers, our goal is to find the rectangular submatrix with the maximum possible sum.

A classical dynamic programming problem can be solved using any of the three approaches.

But keeping in mind the respective time and space complexity, three approaches are discussed here in this article

Approach 1: Using recursion

Output: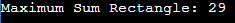

Explanation:

findMaxSumRectangle Function:

This function is responsible for finding the maximum sum rectangle in the input matrix. It uses four nested loops to iterate through all possible submatrices within the matrix. Each submatrix calculates the sum of its elements using the calculateSubMatrixSum function and updates the maximum sum if the calculated sum is greater than the current maximum.

calculateSubMatrixSum Function:

This function calculates the sum of elements within a given submatrix specified by its starting and ending rows and columns. It iterates through the submatrix using two nested loops and accumulates the sum of elements.

In this recursive approach, we iterate through all possible rectangle dimensions (starting row and column, ending row and column) and calculate the sum using the calculateSubMatrixSum method.

Time Complexity: O(n^4)

where "n" is the number of rows or columns in the input matrix.

This approach might fail for larger test cases.

More efficient approaches are discussed further using a concept called dynamic programming.

Since Recursion is the first and foremost step In dynamic programming, We can start thinking about the point of subsequent procedures that need to be followed.

Since there are overlapping subproblems, we can make use of the concept of memoization

Approach 2 : Using memoization

Output: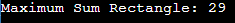

Time Complexity: O(rows^2 * cols^2)

Explanation:

findMaxSumRectangle Function:

This function is responsible for finding the maximum sum rectangle in the input matrix. It uses four nested loops to iterate through all possible submatrices within the matrix. Each submatrix calculates the sum of its elements using the calculateSubMatrixSum function and updates the maximum sum if the calculated sum is greater than the current maximum.

calculateSubMatrixSum Function:

This function calculates the sum of elements within a given submatrix specified by its starting and ending rows and columns. It uses memoization to efficiently compute the submatrix sum using the previously calculated cumulative sum values stored in the memo matrix.

Since the concept of memoization makes use of additional stack space

To eliminate that, a more efficient approach is discussed below, which makes use of a concept called tabulation in dynamic programming

Approach 3 : Tabulation

Output: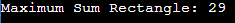

Time Complexity: O(rows^2 * cols^2)

Explanation:

findMaxSumRectangle Function:

This function is responsible for finding the maximum sum rectangle in the input matrix. It utilizes two key steps:

Precomputing Cumulative Sum Matrix (memo):

It initializes a memoization matrix with an extra row and an extra column (memo) to store cumulative sum values for submatrices. The matrix is filled iteratively, and each cell (memo[i][j]) stores the sum of the rectangle formed by the top-left corner ([0][0]) and the bottom-right corner ([i][j]).

Iterating through Submatrices:

It uses four nested loops to iterate through all possible pairs of starting and ending rows and columns of submatrices. For each pair, it calculates the sum of the elements in the corresponding submatrix using the cumulative sum values stored in the memo matrix.

This is the most optimized version of the code.