Find Missing Elements in RangeLet us understand the question using an example. The input for the question will be an array and two integers, low and high. We need to find out the missing elements between low and high. Let us take an example here: If the array is [2,4,6,8,10] and low=5, high=10. The missing values between low and high, i.e., between 5 and 10 in the array, are 6,7,9. So the answer is 6,7,9. So now we need to implement a code to print the values that are not between the given low and high values. CODE: Output: 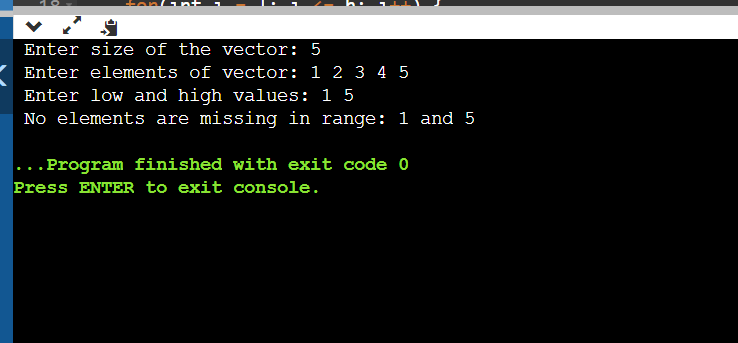
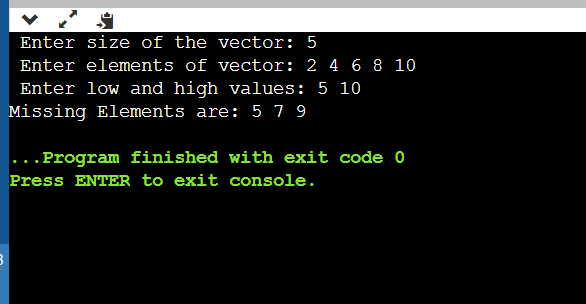
Explanation: First, we now need to take the input for the size of the vector and input elements and store them in a vector. The above lines of code will take the input for the size of the vector, take the vector elements as input, and store them in a vector called vec. Next, we need to prompt the user to enter the low and high values, i.e., in which range we need to find the missing numbers. The above lines of code will handle the case for taking input for l and h values; we need an ans vector to store the missing values in the given range. How to find the missing values, Since the user gives the input of low and high values, we need to iterate from l to h using a loop. Then, for every element between l and h, we need to search for whether the element is present in the vector and to check in the vector, we need to traverse the entire array in the worst case. So, we can easily find out the missing elements between l and h using two for loops. Using the above lines of code, if missing elements are present in the vector, they will be added to the ans vector, or they will not be added. If no elements are added, it implies that no elements are missing in the vector of a given range. Otherwise, we need to print those missing values. Since we have stored the missing values in ans vector, we need to print them now. The above lines of code will print the missing numbers in the given range. Let us discuss the time and space complexity: TIME COMPLEXITY: If we ignore the time taken to take the input, We are traversing from l to h, and for every element in between l and h, we are searching for the element in the vector of size n, so the total taken is: (h-l+1)*n. Then, if any values are missing, we need to print them, and the time taken for it is (h-l+1) in the worst case. So the total time taken is n*(h-l+1) + (h-l+1), and we consider it as n*(h-l+1). SPACE COMPLEXITY: We have taken space for storing the missing values, and in the worst case, the space taken will be (h-l+1) Time complexity: n*(h-l+1) Space complexity: (h-l+1) In the above approach, there is no need for extra space; we can directly print the missing values without storing them in a vector. In the above code, we can directly print them there instead of storing them in a vector, i.e., pushing elements into a vector. In this code, if no elements are printed, we need to assume there were no missing elements. Let us deploy the code for it: CODE: Output: 
Explanation: There is no change from the previous code. We just reduced the space complexity to O(1). But the time complexity remains the same. But we also need to reduce the time complexity, so let us implement the code for reducing the time complexity: CODE: Output: 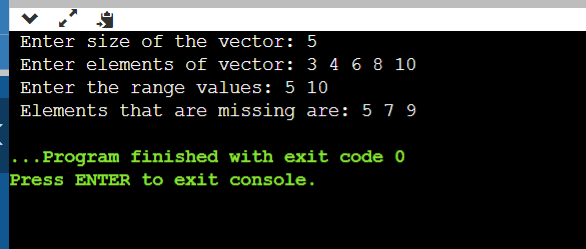
In the above output, the missing elements are printed between 5 and 10 that are not in the input array. 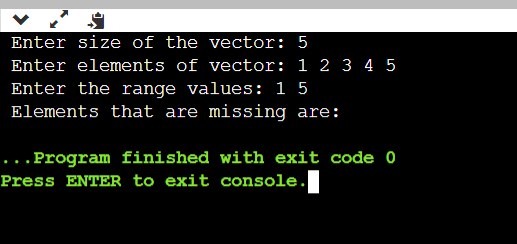
Here, all the values between 1 and 5 are in the given array, so no elements are printed. Explanation: First, we need to take the input for the size of the vector and vector elements, and while taking the elements as input, we also need to insert the values into a map. This is the code to take the size input from the user and vector elements from the user and we also created a map named mp, which will store the values of the vector elements into it. Now, we need to take the input for range values, and then we need to print the missing values between the given range from the given vector. HOW DO WE FIND?We know that searching in a map takes a constant amount of time; we need a loop to iterate from l to h, i.e., range and search for every element if it is present in the map; if the element is not present in the map, then we can say that the element is missing in the given range. The above part of the code will take the input of the range and print all the values that are not present in the vector in the given range. Let us discuss the time and space complexity: TIME COMPLEXITY: If we ignore the time taken for taking the input, we are traversing from l to h, and for each iteration, we are searching for the element in the map which takes time as (h-l+1)*log(N) where n is the size of the map. Time complexity: (h-l+1)*log(n) SPACE COMPLEXITY: Here, we have used space for storing the values into the map, so in the worst case, map size can be n, i.e., the space required is O(N) Space complexity: O(n) We can still optimize the above code; searching for an element takes log(n) time here. Using an unordered set can reduce the time from log(n) to O(1). So, let us implement the code using the unordered set. CODE: Output: 
EXPLANATION: There is no change from the previous code. We have just used an unordered set in place of a map. Let us discuss the time and space complexity: Time complexity: to traverse from l to h in the worst case, h-l can be n, so the time complexity of code is O(N) (here, search in the set takes O(1) time) Space complexity: We use an unordered series, so the space consumed stores its vector elements. So, space complexity is O(N). A short explanation of the previous approaches:
Next TopicK-th Largest Sum Contiguous Subarray
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









