Why is Binary Heap Preferred over BST for Priority Queue?Priority queues are crucial for computer science and many other applications, and two well-liked data structures for implementing them are Binary Heaps and Binary Search Trees (BSTs). We'll go over the reasons why Binary Heaps are frequently chosen for priority queue implementation over BSTs in this in-depth study. Binary heaps are a great fit for priority queues because of their clear temporal complexity for key operations, consistent performance, and ease of use. Consistent and effective performance is a given for developers, which is important in applications that require quick response times. 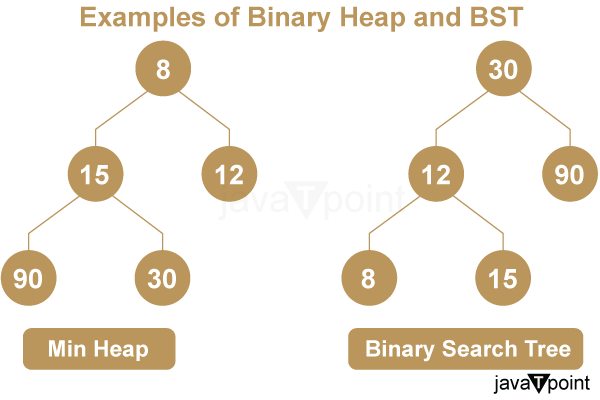
IntroductionThe pieces with the highest (or lowest) priority can be accessed quickly using abstract data types called priority queues. Numerous applications, such as work scheduling and graph algorithms, make use of them. While binary heaps and binary search trees (BSTs) are two popular options, other data structures can also be used to build priority queues. The element with the highest priority is always at the root of a Binary Heap, a specialized tree-based data structure. A Binary Search Tree, on the other hand, is a type of tree-based data structure that makes fast searching and retrieval possible by organizing its components in a predetermined order. We shall examine the advantages of Binary Heaps over BSTs in this post when it comes to implementing priority queues. 1. Simplicity and Predictable PerformanceBinary Search Trees are more complex to implement than Binary Heaps. An array is a useful way to easily represent a Binary Heap, which facilitates management and manipulation. In a Binary Heap, operations such as element insertion and removal have known time-based complexities and are well-defined. For instance, it takes O(log N) time to insert an element into a Binary Heap, where N is the number of elements, and it also takes O(log N) time to remove the element with the highest priority, which is typically the root. Because of these operations' reliable performance characteristics, Binary Heaps are an obvious option for priority queues. The ordering property of Binary Search Trees, however, needs more complex reasoning to be maintained. A skewed BST may eventually degenerate into a linked list with an O(N) time complexity for insertions and deletions, even though the average-case time complexity for these operations in a BST is O(log N). Priority queue implementations find BSTs less appealing due to their unpredictable performance. 2. Space EfficiencyComparing Binary Search Trees to Binary Heaps, the former uses less space. It is not necessary to maintain extra pointers or references between elements because elements in a Binary Heap are stored in a contiguous array. Compared to BSTs, where each node normally needs extra memory for left and right child pointers, this leads to a smaller memory footprint. When there are a lot of pieces in a priority queue, Binary Heaps' space efficiency becomes even more important. Binary heaps are the recommended option for applications where memory usage is a major concern. 3. Efficient Heap OperationsBinary heaps are made to optimize heap-related actions, including shifting an element's priority or inserting and removing the highest priority element. Numerous applications, such as Dijkstra's algorithm for determining the shortest path in a graph, depend on these procedures. After such operations, Binary Heaps are excellent at retaining their attributes and shape, which makes upgrades quick and easy. Although they may perform comparable tasks, Binary Search Trees are not as effective. Because balancing the tree in a BST can be a laborious and complicated process, it is not recommended for situations when the priority queue needs to be updated often. 4. Guaranteed Logarithmic HeightA logarithmic height is guaranteed by Binary Heaps. When N is the number of elements in a Binary Heap, the height of the tree is always O(log N). No matter what order items are placed, this balanced structure guarantees that operations like insertion and deletion require O(log N) time. On the other side, Binary Search Trees are susceptible to imbalance, which can result in worst-case O(N) time complexity for operations such as insertion and deletion. Although self-balancing BSTs like Red-Black and AVL trees help to avoid this problem, their implementation is more complicated. 5. Specific Use-Case Priority Queues:Binary Heaps are designed specifically with priority queues in mind. Their design inherently supports keeping the piece with the highest importance at the top of the heap. Binary heaps are the best option in this circumstance because of how easily priority queues can be implemented and used. Considering their versatility, Binary Search Trees are not well-suited for use cases involving priority queues. Their main benefit is that, although they aren't always required in priority queues, they can facilitate retrieval and searching activities with efficiency. 6. Excellent Performance in PracticeFor priority queue applications, Binary Heaps typically perform better in practice than BSTs. Although Binary Search Trees (BSTs) have an edge in theory when it comes to average-case time complexity for operations, Binary Heaps are generally faster in practice because of their predictable and straightforward nature. BSTs can be less efficient than Binary Heaps due to constant factors and hidden overhead, especially when the priority queue is heavily utilized in applications like operating systems where task scheduling is essential. 7. Binary Heaps vs Fibonacci HeapsIt should be noted that there are more options available for implementing priority queues besides Binary Heaps. For some operations, especially decrease-key operations-which are crucial to algorithms like Dijkstra's shortest path algorithm-Fibonacci Heaps are an additional specialized data structure that provides even better paid-off time complexity. Fibonacci Heaps, however, can be less effective for tiny input sizes because of their greater constant factors and complexity of implementation. Because Binary Heaps balance performance and simplicity, they are a practical option in a variety of situations. 8. Simplicity of Priority Queue AlgorithmsBinary Heap is the foundation of many priority queue algorithms and data structures because of their simplicity. Efficient priority queue operations, including inserting elements and extracting the element with the highest priority, are essential to algorithms like heapsort and Dijkstra's shortest path algorithm. These algorithms can be implemented simply with Binary Heaps, which maintain optimal time complexities. Because of the extra work involved in keeping the tree balanced while managing different operations, implementing comparable algorithms with Binary Search Trees can be more difficult. 9. Ease of Learning and TeachingTo make binary heaps easier for students to learn and comprehend, they are frequently presented in data structure and algorithm courses. They are great for teaching core concepts because of their clear operations and simplicity. Because of its complexity and the requirement to understand ideas like balance, Binary Search Trees might be more difficult for novices to understand even though they are crucial for understanding more advanced tree-based data structures and algorithms. 
10. Wide Adoption and StandardizationMany programming languages and libraries have standardized and commonly used Binary Heaps. The std: priority_queue container, for instance, is provided by the C++ Standard Library and is commonly implemented using a Binary Heap. Developers can now more easily use Binary Heaps as the basis for their priority queues, assuring consistency and interoperability between various applications and systems. This kind of standardization is lacking in Binary Search Trees for priority queue implementations, which can cause inconsistent behavior and performance when utilizing different libraries or custom implementations. 11. Array-Based RepresentationThe indices of the components in an array indicate the parent-child relationships, making it an effective way to describe Binary Heaps. The elements are easy to store and manipulate because to this array-based form, which also streamlines memory management. The heap property of a Binary Heap guarantees that the element with the highest (or lowest) priority is always at the root since the elements are arranged in such a way. In contrast, Binary Search Trees depend on intricate pointer systems among nodes in order to preserve their hierarchical connections. BSTs are less memory-efficient than Binary Heaps because of this pointer-based technique, which uses more memory because each node needs to have left and right child pointers. ConclusionIn summary, Binary Heaps are a better option than Binary Search Trees (BSTs) for creating priority queues. Their numerous and useful benefits make them the best choice in a variety of computer science and application contexts. Binary heaps also have the appealing feature of being efficient in space. Because of their array-based representation, they use less memory, which is especially important when managing large sets of data in a priority queue. On the other hand, because they have more pointers, BSTs use less memory. In reality, Binary Heaps are superior to BSTs because of their ease of use, dependability, and lower overhead-particularly in applications like operating systems where effective task scheduling is crucial. Lastly, the general acceptance and standardization of programming languages and libraries help Binary Heaps, making them more developer-friendly and guaranteeing system interoperability. Essentially, Binary Heaps are the best option for reliable, effective, and broadly usable priority queue systems. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









