Burn the binary tree starting from the target node

Introduction

Burning a binary tree beginning from a particular node is a fascinating issue in computer science, frequently experienced in algorithmic interviews and competitive programming. This task includes reproducing the spread of fire from a given node all through the binary tree and deciding the time it takes for the whole tree to burn.

In this article, we will discuss into different ways to deal with and tackle this issue utilizing the C programming language. Prior to delving into the solutions, we should get a handle on the problem statement. We're given a binary tree, where every node contains a value, and we really want to start a fire at a particular objective node. The fire spreads from the objective node to its adjacent nodes (left and right children) and keeps spreading until all nodes are burnt. Our goal is to ascertain the time it takes for the whole tree to burn down.

Depth-First Search

One of the intuitive solutions for this issue includes utilizing a Depth-First Search traversal technique. We can recursively traverse the tree, beginning from the objective node, and monitor the time it takes for the fire to arrive at each node.

Code

Output: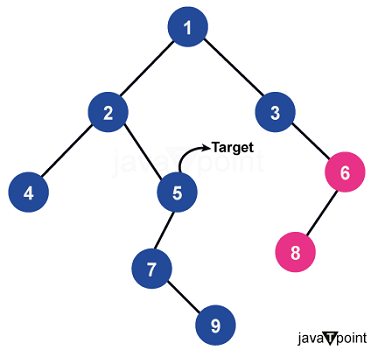

Code Explanation

Structure Definition

• A structure TreeNode is characterized to address each node in the binary tree. It contains an integer value (val) and pointers on its left and right children.

Max Function

• This function returns the maximum of two numbers.

DFS Function

• This function plays out a Depth First Search traversal of the binary tree. It takes the ongoing node, target node value, and distance from the objective node as parameters.
• Assuming the ongoing node is Invalid, it brings 0 back.
• Assuming thevalue of the ongoing node matches the objective node esteem, it returns the distance.
• In any case, it recursively calls DFS on the left and right children, updating the distance likewise, and returns the greatest distance acquired from the children.

BurnTime Function

• This function ascertains the time it takes to burn the whole binary tree beginning from the objective node.
• Assuming that the root is Invalid or the root's value matches the objective node, it brings 0 back.
• It then calls the DFS function on the left and right subtrees, beginning from the root, and returns the most extreme distance from both subtrees.

Main Function

• In the main function, memory is allocated for the root node and its children.
• The values of the nodes are allocated.
• The objective node value is set.
• The burnTime function is called with the root node and target node value as arguments, and the outcome is printed.
• Memory allotted for the nodes is liberated to prevent memory leaks.

Conclusion

Burning a binary tree beginning from a particular node presents an intriguing algorithmic test. In this article, we investigated the issue of articulation and examined one of the ways to deal with addressing it by utilizing Depth first search in the C programming language. The provided C code scrap exhibits how to execute this methodology and calculate the time it takes for the whole tree to burn beginning from a given objective node. Seeing such issues upgrades our critical thinking abilities as well as reinforces our grip on tree traversal algorithms.