DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
The sum of Elements Between k1th and k2th smallest elementsWe need to find the sum of the elements between the given two indexes of the given vector. Where the user provides the two indexes and the input vector. Let us understand through an example: If the vector is [ 1 4 2 6 8 11 10] and k1, k2 are 2,5. Here, we must find the sum of numbers between the k1 and k2 indexes. But first, we need to sort the given vector and sum the values from the k1 to the k2 index. So, after sorting, the vector becomes as follows: [1 2 4 6 8 10 11]. If we consider the indexes form 0, the sum of values from index 2 to index 5 is 4+6+8+10 = 28. Now we need to implement a code to find the sum of values between the k1 and k2 index, including the k1 and k2 indexes: CODE: Output: 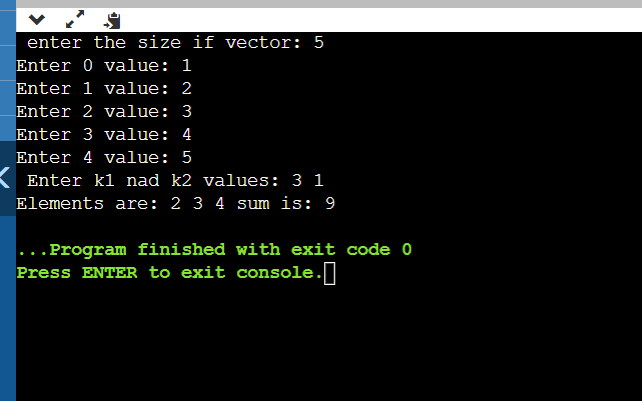
Explanation: First, we have included the required libraries for the execution of the code. This part of the code will take the vector elements as input and get stored in the vector named vec. Next, we need to sort the vector to easily traverse the smallest elements from The above line of code will sort the given input vector, where sort is an inbuilt function that takes parameters as the address of the vector beginning and ending. Next, we need to prompt the user to enter the k1 and k2 indexes to find the sum of elements between the k1 and k2 indexes. This part of the code will handle taking input for ka and k2 values, and we also swap k1 k2 if k2<k1 because if k2<k1, we cannot iterate through the loop. So, we swapped both elements. Next, we need to calculate the sum from index k1 to index k2, and we will also print the values that make that sum. The above loop calculates the sum of elements between the k1 and k2 indexes, including k1 and k2 indexes. It will also print the elements that are making the sum. And finally, we will print the sum of values from index k1 to index k2. We will also handle cases where the user gives a k1 or k2 value greater than or equal to n. In this case, we cannot calculate the sum because we will get an error called vector index out of bound, i.e., we are trying to access the elements that are not in the vector. The below code is responsible for handling those cases. Output for handling this case is: 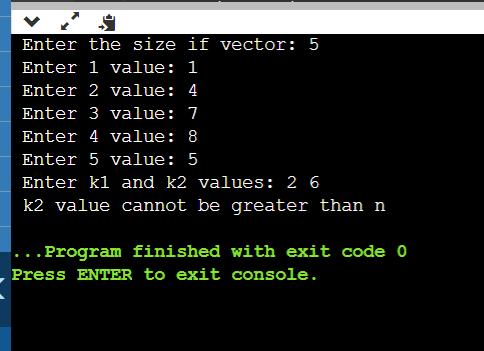
Time and space complexity: Tim complexity: O(N*log(N)) for sorting the vector to calculate the sum in worst case O(N). Total time complexity is O(N)+O(N*log(N)). Space complexity: If we don't consider the space for input, then the code takes a constant amount of space.
Next TopicPrint Matrix in a Snake Pattern
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









