Application of Binary Tree

The common non-linear data structure known as a tree. A tree illustrates a hierarchical structure in contrast to other data structures such an array, stack, queue, and linked list, which are linear in nature. A tree's ordering information is irrelevant. Two pointers and nodes make up a tree. The parent node's left and right children are represented by these two pointers. Let's thoroughly comprehend the words used in trees.

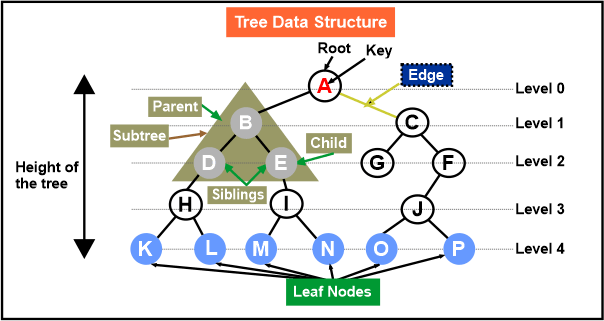
• The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
• Parent Node: A node's parent one is the node that came before it in the tree of nodes.
• Child Node: The node that is a node's direct successor is referred to as a node's child node.
• Siblings are the children of the same parent node.
• Edge: Edge serves as a connecting node between the parent and child nodes.
• Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
• A node's subtree is the tree that views that specific node as the root node.
• Depth: The depth of a node is the separation between it and the root node.
• Height: The height of a node is the distance between it and the subtree's deepest node.
• The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
• Level: In the tree, a level is the number of parents that correspond to a particular node.
• Node degree: A node's degree is determined by how many children it has.
• A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.

Why use a tree-based data structure?

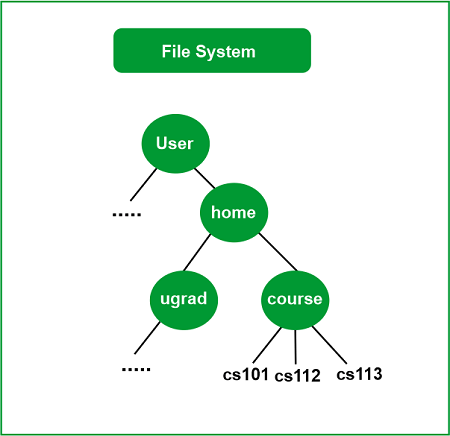
1. You might wish to store information that naturally develops a hierarchy, which is one reason to use trees. For instance, a computer's file system:
   
2. Trees offer reasonable access/search (with some ordering, like BST) (quicker than Linked List and slower than arrays).
3. Trees offer limited insertion and deletion (quicker than Arrays and slower than Unordered Linked Lists).
4. Because pointers are used to connect nodes, trees, like linked lists, have no maximum number of nodes.

The primary uses for tree data structures include:

• Manipulation of data in hierarchies.
• Make information searchable (see tree traversal).
• Manipulate data-sorted lists.
• For the purpose of composing digital pictures for visual effects.
• Routing protocols
• Multi-stage decision-making process type (see business chess).

What is a Binary Tree?

A binary tree is a tree data structure made up of nodes also known as left and right nodes-each of which has a maximum of two offspring. The tree starts at the root node.

Binary Tree Representation

Each node in the tree has the following information:

• Pointer to the left child
• Pointer to the right child

In C, we may use structures to represent a tree node. We may utilise classes as a component of other languages' OOP features. An illustration of a tree node containing integer data is shown below.

Application of Binary Tree

• Binary trees are applied in data compression methods in the form of the Huffman coding tree.
• Expression Trees, a binary tree application, are used in compilers.
• Another binary tree application that searches maximum or minimum in O(log N) time complexity is priority queue.
• Display data that is hierarchical.
• Utilized in spreadsheet and Microsoft Excel editing applications.
• Syntax trees are used by several well-known computer compilers, including GCC and AOCL, to execute arithmetic operations. They are helpful for indexing segmentation at the database and storing cache in the system.
• For putting priority queues into action.
• Utilized to provide quick memory allocation in computers (binary search tree) by finding items more quickly.
• Encoding and decoding operations

Binary tree Basic Operations

• Eliminating a component
• Looking for a component.
• Elimination of an element.
• Crossing a boundary. A binary tree has four (usually three) different forms of traversals, which will be covered in the following paragraphs.

Binary tree auxiliary operations

• Calculating the tree's height
• Determine the tree's level.
• Calculating the overall tree's size.

Binary Tree's benefits include

• A binary tree's searching process is incredibly quick.
• A binary tree can be represented in a straightforward and understandable way.
• It is effectively done to go from a parent node to its child node and vice versa.
• Simple to comprehend and apply.
• A pyramidal organization.
• The data set's structural links should be reflected
• Compared to data storage, inserting data is simple.
• Data storage in memory management is simple.
• The user can quickly execute numerous nodes.
• Arbitrary number of data values can be stored.

Binary Tree disadvantages:

• Many pointers in binary tree traversals are null and hence worthless.
• A Binary Search Tree (BST) access operation takes longer than an array access operation.
• Depending on the height of the tree, there are few basic options.
• Node deletion is difficult.
• The height of the tree is one simple choice.