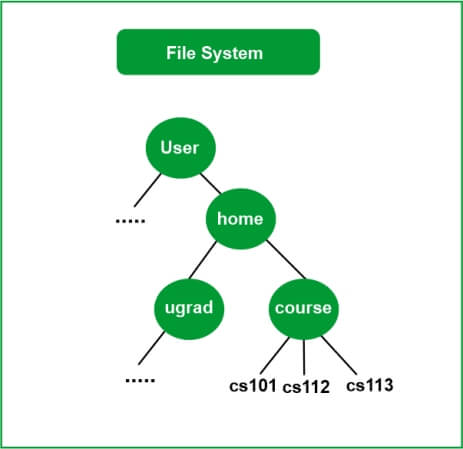
Properties of Binary Tree

The common non-linear data structure known as a tree. A tree illustrates a hierarchical structure in contrast to other data structures such an array, stack, queue, and linked list, which are linear in nature. A tree's ordering information is irrelevant. Two pointers and nodes make up a tree. The parent node's left and right children are represented by these two pointers. Let's thoroughly comprehend the words used in trees.

• The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
• Parent Node: A node's parent one is the node that came before it in the tree of nodes.
• Child Node: The node that is a node's direct successor is referred to as a node's child node.
• Siblings are the children of the same parent node.
• Edge: Edge serves as a connecting node between the parent and child nodes.
• Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
• A node's subtree is the tree that views that specific node as the root node.
• Depth: The depth of a node is the separation between it and the root node.
• Height: The height of a node is the distance between it and the subtree's deepest node.
• The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
• Level: In the tree, a level is the number of parents that correspond to a particular node.
• Node degree: A node's degree is determined by how many children it has.
• A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.

The primary uses for tree data structures include:

• Manipulation of data in hierarchies.
• Make information searchable (see tree traversal).
• Manipulate data-sorted lists.
• For the purpose of composing digital pictures for visual effects.
• Routing protocols
• Multi-stage decision-making process type (see business chess).

What is a Binary Tree?

A binary tree is a tree data structure made up of nodes also known as left and right nodes-each of which has a maximum of two offspring. The tree starts at the root node.

Binary Tree Representation

Each node in the tree has the following information:

• Pointer to the left child
• Pointer to the right child

In C, we may use structures to represent a tree node. We may utilise classes as a component of other languages' OOP features. An illustration of a tree node containing integer data is shown below.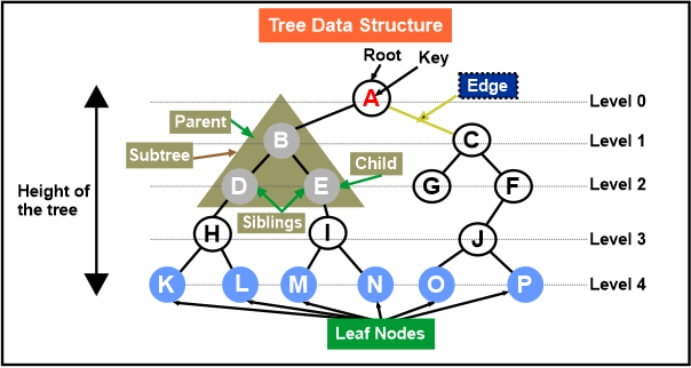

Why use a tree-based data structure?

1. You might wish to store information that naturally develops a hierarchy, which is one reason to use trees. For instance, a computer's file system:
   
2. Trees offer reasonable access/search (with some ordering, like BST) (quicker than Linked List and slower than arrays).
3. Trees offer limited insertion and deletion (quicker than Arrays and slower than Unordered Linked Lists).
4. Because pointers are used to connect nodes, trees, like linked lists, have no maximum number of nodes.

Properties of Binary Tree

1. In a binary tree, level 'l' can have up to 2l nodes:

Note: In this case, level refers to the quantity of nodes along the route from the root to the node (including root and node). The root's level is 0.

This is demonstrable by induction:

Root l = 0, 20 nodes = 1 for root

Assume there are 2l nodes at most on level "l."

Since each node in a binary tree may only have two offspring, the subsequent level would have twice as many nodes, or 2 * 2l.

2. There can be a maximum of 2h - 1 nodes in a binary tree of height "h":

Notably, the maximum number of nodes along the root-to-leaf path determines a tree's height in this case. A tree with a single node is regarded as having a height of 1.

This outcome follows from the second point above. If all levels have the maximum number of nodes, the tree has reached its maximum number of nodes. Therefore, there may be a maximum of 1 + 2 + 4 +.. + 2h-1 nodes in a binary tree of height h. This is a straightforward geometric series with h terms, and its total is 2h-1.

The height of the root is regarded as zero in certain texts. In this case, the formula above becomes 2h+1 - 1.

3. The smallest height or smallest number of levels in a binary tree with N nodes is Log2(N+1):

Since each level must include at least one element, the height cannot exceed N. The most nodes that a binary tree of height "h" may have is 2h - 1. (previous property). Consequently, there won't be as many nodes as this many or more.

N <= 2h - 1

2h >= N+1

log2(2h) >= log2(N+1) (Taking log both sides)

hlog22 >= log2(N+1) (h is an integer)

h >= | log2(N+1) |

So the minimum height possible is | log2(N+1) |

4. There are at least | Log2L |+ 1 levels in a binary tree with L leaves:

When all levels are completely filled, a binary tree has the most leaves (and the fewest levels). If all leaves are at level L, then the formula below holds for L leaves.

L <= 2l-1 [From Point 1] [Note: Here, consider level of root node as 1]

l = | Log2L | + 1

where l is the minimum number of levels.

5. The number of leaf nodes is always one more than nodes with two children in a binary tree where each node has 0 or 2 children:

L = T + 1

Where L = Number of leaf nodes

T = Number of internal nodes with two children

Proof:

No. of leaf nodes (L) i.e. total elements present at the bottom of tree = 2h-1 (h is height of tree)

No. of internal nodes = {total no. of nodes} - {leaf nodes} = { 2h - 1 } - {2h-1} = 2h-1 (2-1) - 1 = 2h-1 - 1

So , L = 2h-1

T = 2h-1 - 1

Therefore L = T + 1

Hence proved

6. If n is the total number of nodes and e is the total number of edges in a non-empty binary tree, then e = n-1:

Except for the root node, every node in a binary tree has precisely one parent. So n-1 nodes have precisely one parent if n is the entire number of nodes. Every child and its parent share the same edge. Thus, there are n-1 edges overall.

Application of Binary Tree

• Binary trees are applied in data compression methods in the form of the Huffman coding tree.
• Expression Trees, a binary tree application, are used in compilers.
• Another binary tree application that searches maximum or minimum in O(log N) time complexity is priority queue.
• Display data that is hierarchical.
• Utilized in spreadsheet and Microsoft Excel editing applications.
• Syntax trees are used by several well-known computer compilers, including GCC and AOCL, to execute arithmetic operations. They are helpful for indexing segmentation at the database and storing cache in the system.
• For putting priority queues into action.
• Utilized to provide quick memory allocation in computers (binary search tree) by finding items more quickly.
• Encoding and decoding operations

Binary Tree's benefits include

• A binary tree's searching process is incredibly quick.
• A binary tree can be represented in a straightforward and understandable way.
• It is effectively done to go from a parent node to its child node and vice versa.
• Simple to comprehend and apply.
• A pyramidal organization.
• The data set's structural links should be reflected
• Compared to data storage, inserting data is simple.
• Data storage in memory management is simple.
• The user can quickly execute numerous nodes.
• Arbitrary number of data values can be stored.

Binary Tree disadvantages:

• Many pointers in binary tree traversals are null and hence worthless.
• A Binary Search Tree (BST) access operation takes longer than an array access operation.
• Depending on the height of the tree, there are few basic options.
• Node deletion is difficult.
• The height of the tree is one simple choice.