Sort an Array of 0's, 1's, and 2's

The array is a linear data structure that contains the elements at the contiguous memory location. It mainly stores the elements of the same data type together at such locations. The difference between these consecutive memory locations depends on the type of data we are using, whether int, float, double, char, long, etc. The elements present at consecutive memory locations make it easier for us to track the elements. It also reduces our complexity to search an element compared to other data structures like Linked list, Queue, Stack, and Non-Linear Data structures like trees and graphs.

One can choose the base index of an array easily. Usually, programming languages allowing n-based indexing also allow negative index values, and other scalar data types like enumerations or characters may be used as an array index. The array contains the index, which starts with 0 and ends up to the size of the array minus one. If we have an array of 12 elements, then the index of the array will start from 0 and end up to index number 11.

Sorting an array implies that the elements present in the array must be present in a particular order, whether in ascending order or in descending order. For example, if we take the array of 5 elements as follows - 4, 2, 3, 10, 5. Now, if I want this array to be sorted in order, then it will arrange in ascending order by default, and the result will be - 2, 3, 4, 5, 10. We will use various sorting methods to sort the elements of an array, such as Bubble sort, Insertion sort, Quick sort, and Merge sort. Among these complexities, Quicksort and Merge sort play a very important role in sorting methods.

What are an array of 0s, 1s, and 2s?

As we have already seen, that array is a linear data structure containing the data of the same data type present at the consecutive memory location. Here in this 0s, 1s, and 2s array, we will only store the data in the 0s, 1s, and 2s form. For example, an array containing 11 elements and these elements are as follows - 0, 1, 1, 2, 2, 1, 0, 2, 1, 0, 0.

If we talk about sorting the array containing elements in the form of 0s, 1s, and 2s, it means arranging the elements of an array in ascending or descending order. Here we will consider ascending order as a default case. Let us take a new array of 10 elements, which contains the elements in 0s, 1s, and 2s.

The main task we need to perform is to sort an array so that all 0's come before all the ones and all one's come before all the two's, and at last, all two's will fill out the remaining array.

A = { 0, 1, 2, 2, 0, 1, 0, 2, 1, 0 }

Sorted version of Array A = { 0, 0, 0, 0, 1, 1, 1, 2, 2, 2 }

B = { 0, 1, 2, 1, 0, 1, 0, 2, 1, 0 }

Sorted version of Array B = { 0, 0, 0, 0, 1, 1, 1, 1, 2, 2 }

Methods of sorting of an 0's, 1's and 2's array -

1. By Brute force method using double traversal.
2. Using an efficient approach using a single traversal method named the three-way partitioning

Let us start sorting an array using these methods -

Method # 1 - Brute force approach using double traversal

Using this method, we need to sort the array containing 0's, 1's, and 2's in ascending order. However, it depends on the programmer to sort an array in ascending or descending order; we will sort the array in the default case, i.e., ascending order.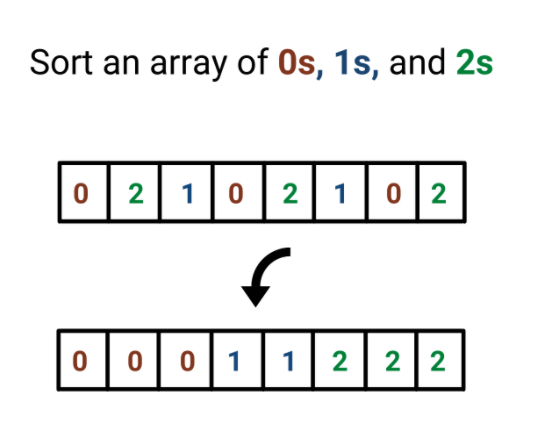

We will derive the algorithm for the ' n ' number of elements, but we will take a random array and experiment with it for our basic understanding of the concept.

A = { 0, 1, 0, 2, 1, 1, 0, 2, 2, 0, 1 }

Procedural steps -

1. First of all, count the total number of elements in the given array; here, we have given an array of 11 elements.
2. Scan the elements of the array from left to right and trace the elements one by one.
3. Then count the count number of 0's present in the array and store it in a variable.
4. Similarly, in this way, count the number of 1's present in the array and store them in another variable.
5. At last, count all numbers of 2's present in the array and store the count in another variable. Or, to know the number of 2's present in an array, you can deduct the number of counts of 0's and 1's from the total number of elements present in the array.
6. You can do the criteria in this example only because we already know the array, but if the user enters the elements of an array in runtime. You are not sure the values entered by the user are all in the form of 0's, 1's, and 2's only until the user is bound with the condition of that to enter the values only in the form of 0's, 1's, and 2's.
7. Here in the above example, we have 4 0's, 4 number of 1's, and 3 number of 2's.
8. After counting several 0's, 1's, and 2's present in the array, then copy the values one by one again in array A.
9. For copying the values, start a loop that initially points to the 0^th index of an array; first, copy all numbers of 0's present in the array and simultaneously increment the index value. All the 0's will be copied up to the index number 3.
10. Then for copying all numbers of 2's, start the pointer that points to the index 4, because at indexes 0 to 3, we have all 0's present. Now, copy all the number of 1's in the array and simultaneously increase the index one by one. We have in the above example; 4 numbers of 1's; hence after copying all ones, our index will reach the 7.
11. For copying all the number of 2's in the array, start the index from 8 because till index 7 we have all number of 0's and after then we have all number of 1's present in it. Now copy all the numbers of 2's in the array and simultaneously increase the index one by one. We have in the above example; 3 numbers of 2's; hence after copying all twos, our index will reach 10.
12. Therefore, in the end, we are succeeded in copying all the numbers of 0's, 1's, and 2's in the array in ascending order.

Algorithm for sorting an array containing elements in the form of 0's, 1's, and 2's in the ascending order using counting method, i.e., Method # 1.

Step 1 - Consider an array of n elements, and all elements are in the form of 0's, 1's, and 2's.

Step 2 - Construct a function of sorting array of 0s, 1s, and 2s.

Step 3 - Pass array and a total number of elements in the sorting function as an argument from the main function.

Step 4 - In the sorting function, declare three variables named zero counts, onecount and twocount.

Step 5 - The variable zero count stores the count of all zeros present in the array passes from the main function as an argument.

Step 6 - The variable onecount stores the count of all present in the array passes from the main function as an argument.

Step 7 - The variable twocount stores the count of all twos present in the array passes from the main function as an argument.

Step 8 - After counting all 0s, 1s, and 2s from the array, insert all the values back into the given main array because we need to sort the array.

Step 9 - Initially, put all the zeros back into the array, which is passed as an argument in the main function.

Step 10 - After putting all zeros from the continuing index number, insert all the ones back into the array.

Step 11 - Similarly, at last, put all the twos back into the array on the remaining indexes.

Step 12 - At last, in the main function, print the sorted array.

Now let us execute above method 1, i.e., Brute force double traversal method in C, C++, and Python.

Program of sorting of an array containing 0's,1's, and 2's using method 1 in C Programming Language -

The output of the following C program for sorting the array of 0's, 1's, and 2's using Method # 1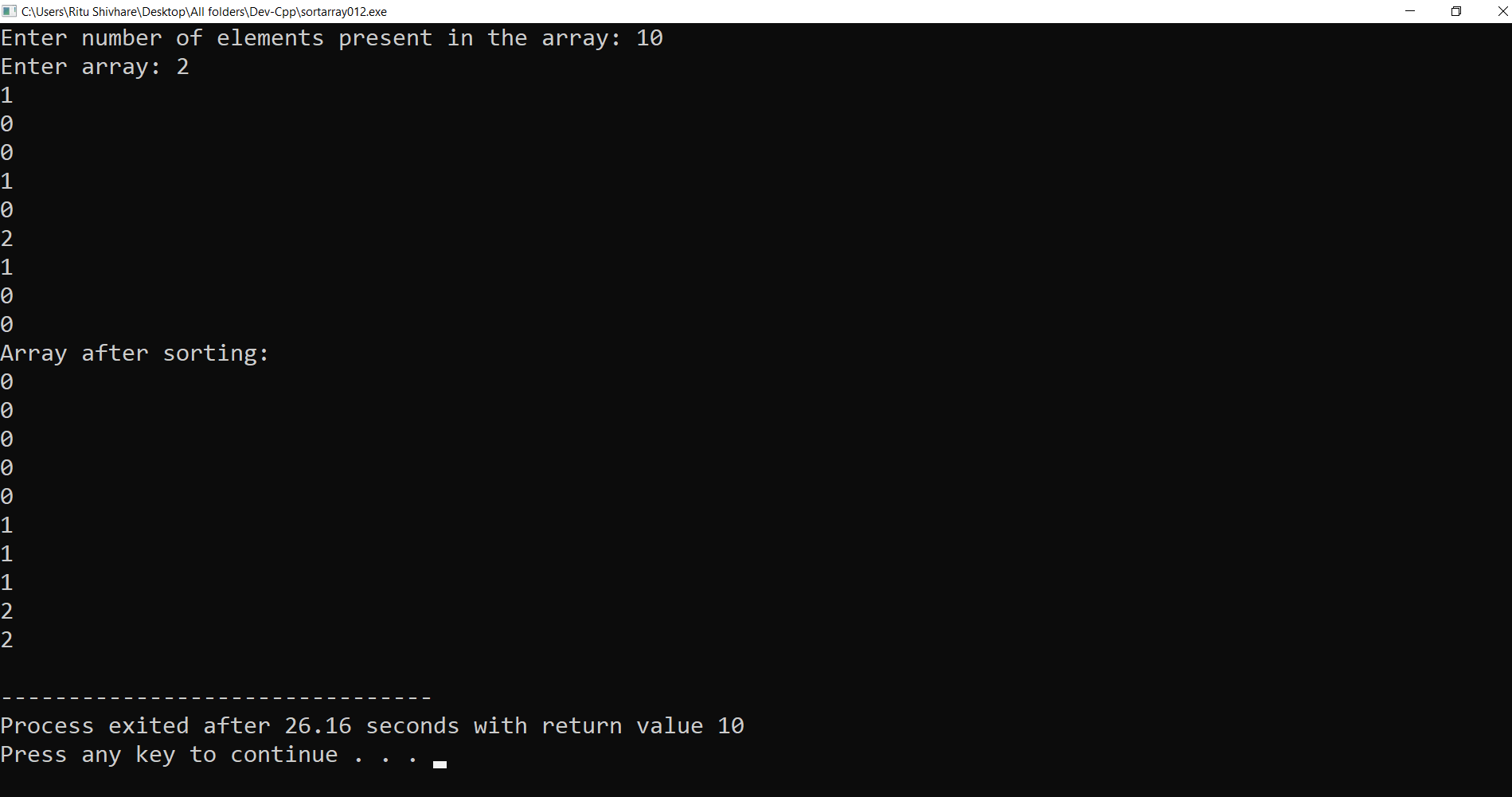

Program of sorting of an array containing 0's,1's, and 2's using method 1 in C++ Programming Language -

The output of the following C++ program for sorting the array of 0's, 1's, and 2's using Method # 1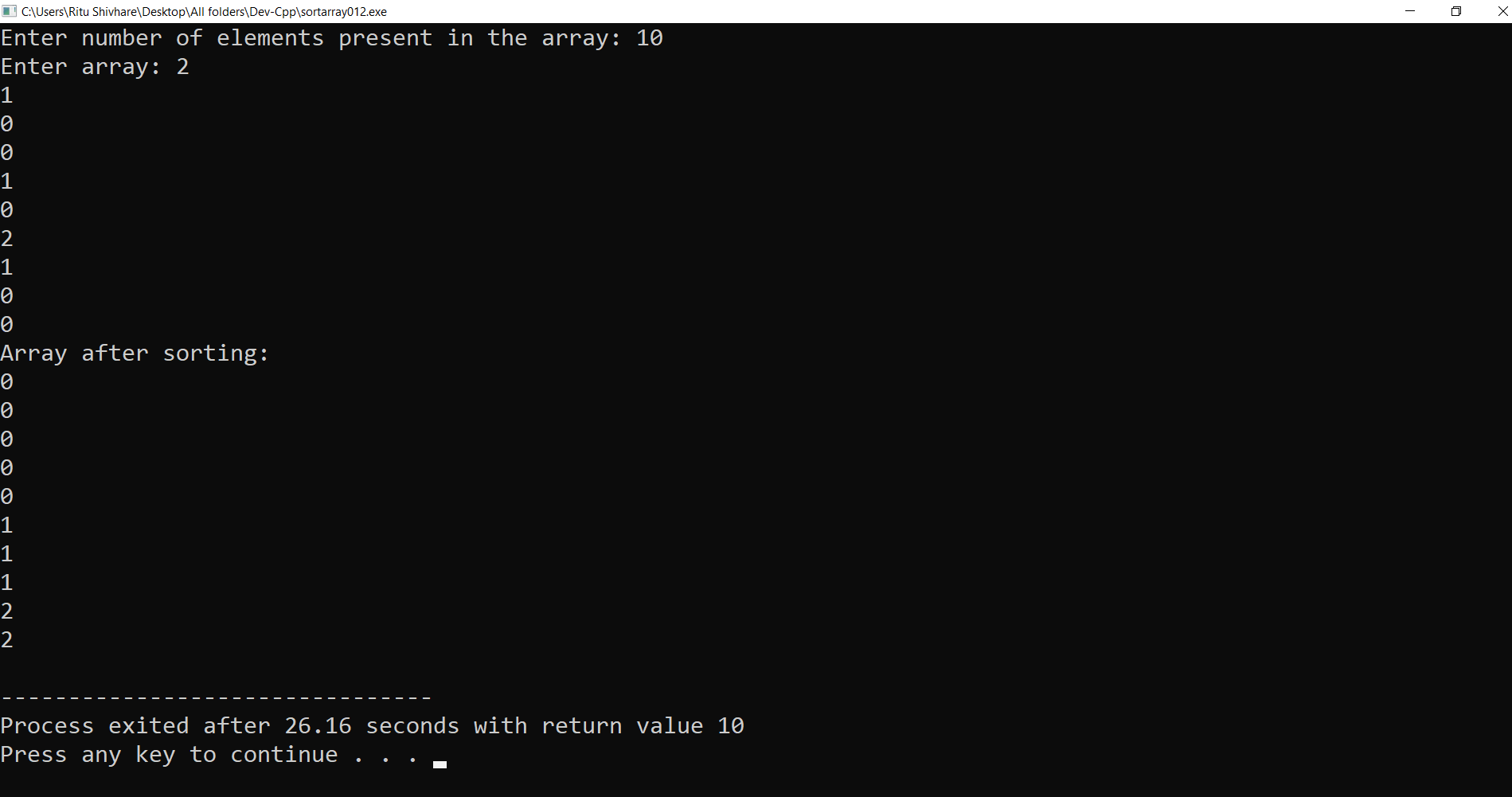

Program of sorting of an array containing 0's,1's, and 2's using method 1 in Python Programming Language -

The output of the following Python program for sorting the array of 0's, 1's, and 2's using Method # 1

Program of sorting of an array containing 0's,1's, and 2's using method 1 in Java Programming Language -

The output of the following JAVA program for sorting the array of 0's, 1's, and 2's using Method # 1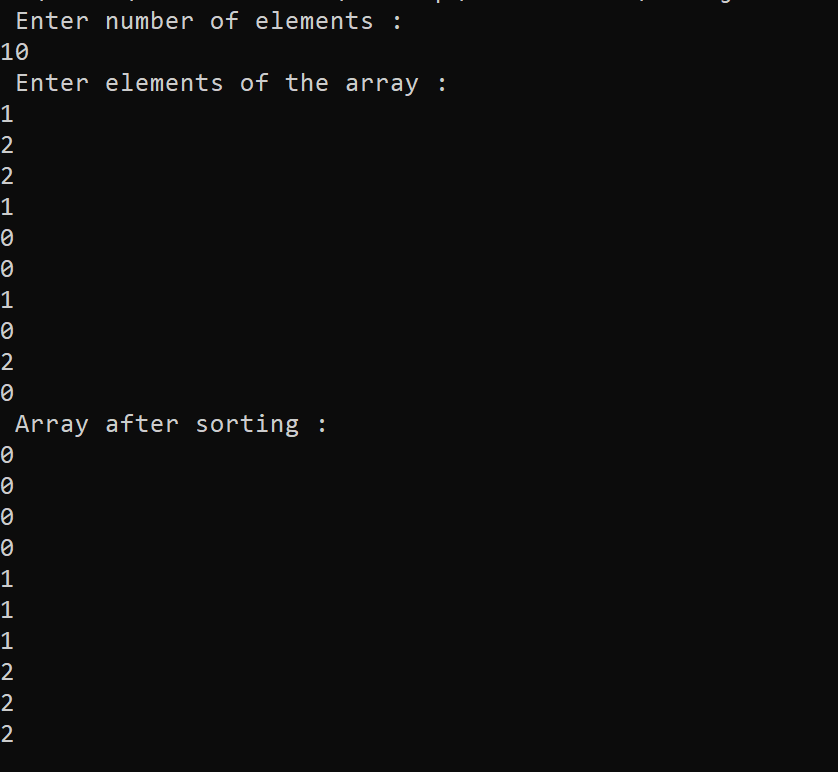

After executing the program successfully in a specific programming language and following the Brute force algorithm using the double traversal approach, we will get the proper result, i.e., sorting an array in ascending order.

Now let us analyze the running time and performance of the algorithm we are applying to sort the array in ascending order by finding the algorithm's time complexity and space complexity using in Method # 1.

Time Complexity of Method # 1 -

For finding the time complexity, we need to observe the algorithm and analyze the time taken by a particular line for execution. We can observe that we require traversing the array twice; one traversal counts the number of 0's, 1's, and 2's. After counting, the second traversal is done to copy back the sorted values in the array, and for this, we need to copy n elements. Hence time complexity will be -

T ( n ) = O ( n ) + O ( n )

T ( n ) = O ( n )

Hence time complexity will be O ( n ) , as we do the asymptotically rough idea that we require ' n ' time to solve the problem of ' n ' elements.

Space Complexity of Method # 1 -

To find space complexity, we need to observe the program and analyze the space required to store all the variables. As we notice the program, we will observe that no extra space is required to store the elements.

S ( n ) = O ( 1 )

Hence the space complexity for above method # 1 will be constant.

Method # 2 - By applying an optimized method of three-way partitioning using Single Traversal

By using this method, we need to sort the array, containing 0's, 1's, and 2's, in ascending order; However, it depends on the programmer whether they want to sort an array in ascending or descending order; we will here sort the array in the default case, i.e., ascending order.

At first, in every programmer's mind, the approach of method 1 comes, we will first traverse the array and then count the number of 0's, 1's, and 2's from the elements given in the array in single traversal. We will again do traversal of an array and copy the elements in the array on the sequential basis. Finally, as we have already seen above, we need to do two times traversal of the given for sorting the elements of an array.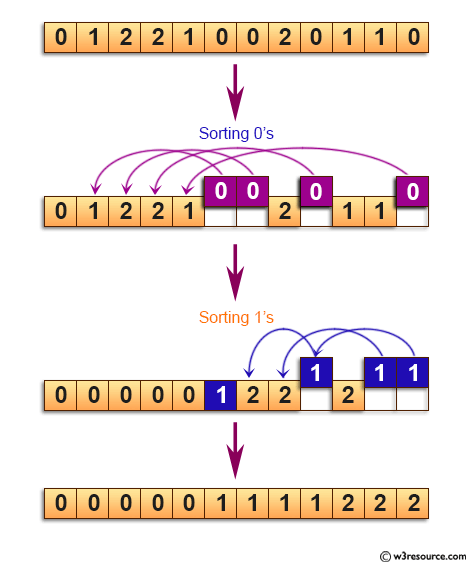

In this Three-way partitioning method, we need to traverse only a single time, and while in this traversing, we will sort the whole array in ascending order. This approach will divide the array into four sections using three-pointers, i.e., Low, Mid, and High.

The four pointers are as follows -

1. Section 1 - Before the Low pointer, i.e., 0 to low - 1, we have the particular section of the array in which we have all elements whose values are 0.
2. Section 2 - After low and before mid, i.e., low to mid - 1, we have another particular section of the array in which we have all elements, whose values are 1.
3. Section 3 - After mid and before high, i.e., mid to high - 1, we have another section of the array in which we have all elements whose values are unknown to us, hence the values that we cannot predict.
4. Section 4 - After high and it will reach n-1, means up to the last index of the given array, i.e., high to n - 1, we have the last particular section of the array in which we have all elements, whose values are 2.

Consider one thing before partitioning every section that partitioning is done based on a particular criterion, i.e., let us take section 1; in section 1, we need to divide the array in a section that starts from index 0, and it ends up too low -1. We can define the range of it as - [ 0, low ), which means that we do not include the index ' low ' in Section 1.

Similarly, in section 2, we can define the range from low to mid - 1, i.e., [ low, mid ), implying that we cannot include the index with the number ' mid '.

In the same way, we have the range of section 3, i.e., [ mid, high ), which implies that we cannot include the index which has the number ' high '.

At last, we can define the range of the last section 4, i.e., [ high, n ), which implies that we cannot include the index which has the number ' n '.

We will derive the algorithm for the ' n ' number of elements, but we will take a random array and experiment on it for our basic understanding of the concept.

A = { 0, 1, 0, 2, 1, 1, 0, 2, 2, 0, 1 }

Procedural steps -

1. First of all, count the total number of elements in the given array; here, we have given an array of 11 elements.
2. We need three-pointers that divide the array into four sections, as we saw the mechanism of the four sections above.
3. At the starting point, we could not differentiate whether which section contains all zeros and which contains all ones, and only twos.
4. Hence initially, we will start the two pointers from index 0 in such a way that low = 0 and mid = 0.
5. For high, we start pointing it from the last index of the given array, i.e., high = 11 - 1 = 10.
6. After that, we will run the loop, from mid to high, pointing from 0 to 10, as per the above example.
7. We will check the mid pointer pointing to that particular index in the given array in this loop.
8. If the mid pointer points to the value 0, we will first swap the values present at pointer mid with the values present at pointer low. After that, we will increment the pointer low by 1 and mid by 1 and continue the loop.
9. If the mid pointer points to the value 1, we will increase the mid by 1 and continue the loop.
10. If the mid pointer points to the value 2, we will first swap the values present at pointer mid with the values present at pointer high. After that, we will decrement the pointer high by 1 and continue the loop.
11. This loop will process till the mid reaches to pointer high.
12. Hence finally, we will find the sorted array as a result.

Algorithm for sorting an array containing elements in the form of 0's, 1's, and 2's in the ascending order using counting method, i.e., Method # 2.

Step 1 - Consider an array of n elements, and all elements are in the form of 0's, 1's, and 2's.

Step 2 - Construct a function of sorting array of 0s, 1s, and 2s.

Step 3 - Pass array and a total number of elements in the sorting function as an argument from the main function.

Step 4 - In the sorting function, declare three variables named low, mid, and high.

Step 5 - Initialize these variables as low = 0, mid = 0 and high = n - 1.

Step 6 - Run the loop till mid<=high.

Step 7 - If A [ mid ] == 0, then we do swap the elements present at index low with the element present at index mid, and after then increment the low by 1 as low = low + 1, and increment the mid by 1 as, mid = mid + 1.

Step 8 - continue.

Step 9 - If A [ mid ] == 1, then we do increment the mid by 1 as, mid = mid + 1.

Step 10 - continue

Step 11 - If A [ mid ] == 2, we swap the elements present at index mid with the element present at index high, and after then decrement the high by 1 as high = high - 1.

Step 12 - continue.

Step 13 - At last, finally print the sorted array in the main function.

Now let us execute above method 1, i.e., Brute force double traversal method in C, C++, and Python.

Program of sorting of an array containing 0's,1's, and 2's using method 2 in C Programming Language -

The output of the following C program for sorting the array of 0's, 1's, and 2's using Method # 2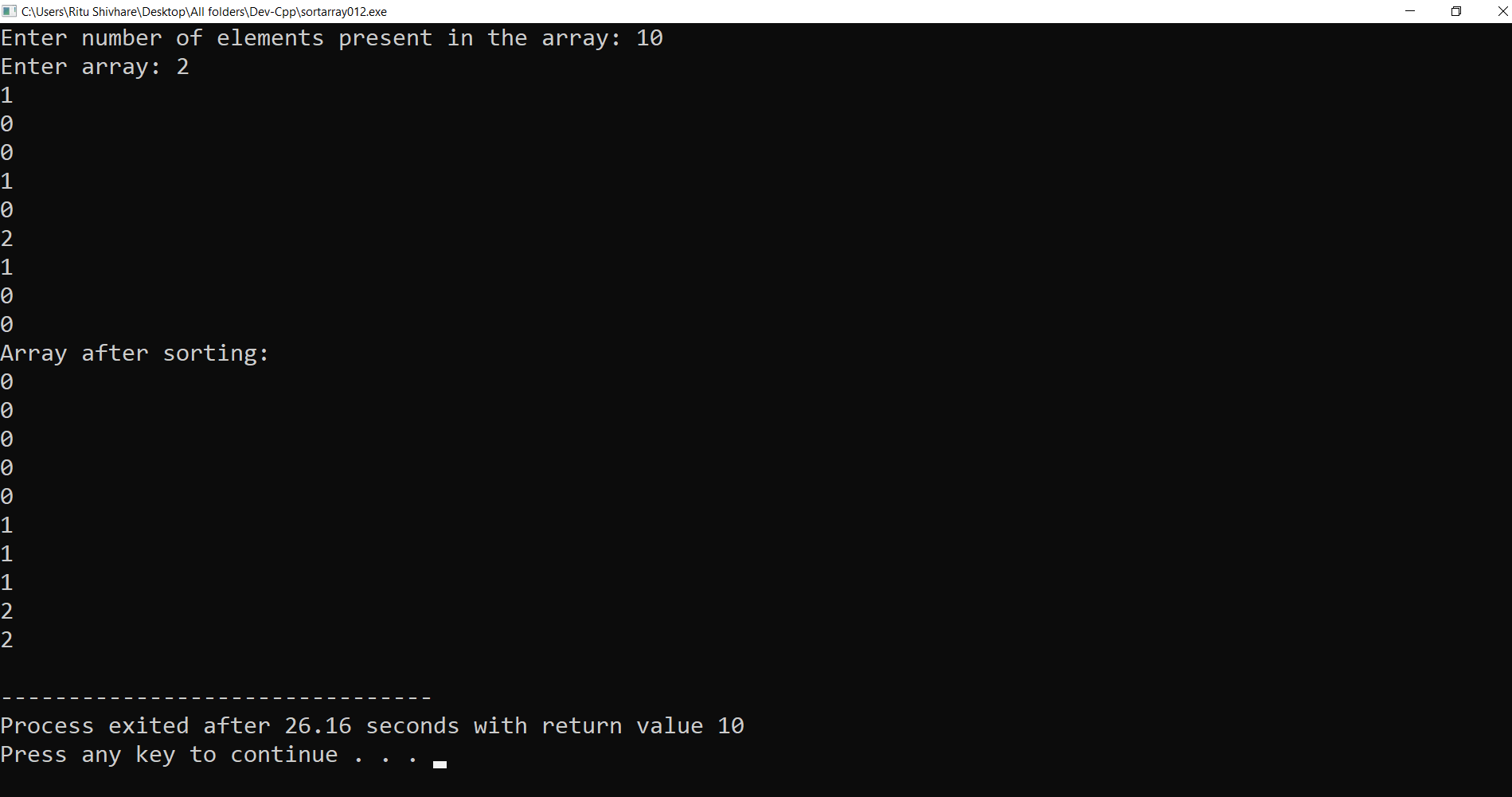

Program of sorting of an array containing 0's,1's, and 2's using method 2 in C++ Programming Language -

The output of the following C++ program for sorting the array of 0's, 1's, and 2's using Method # 2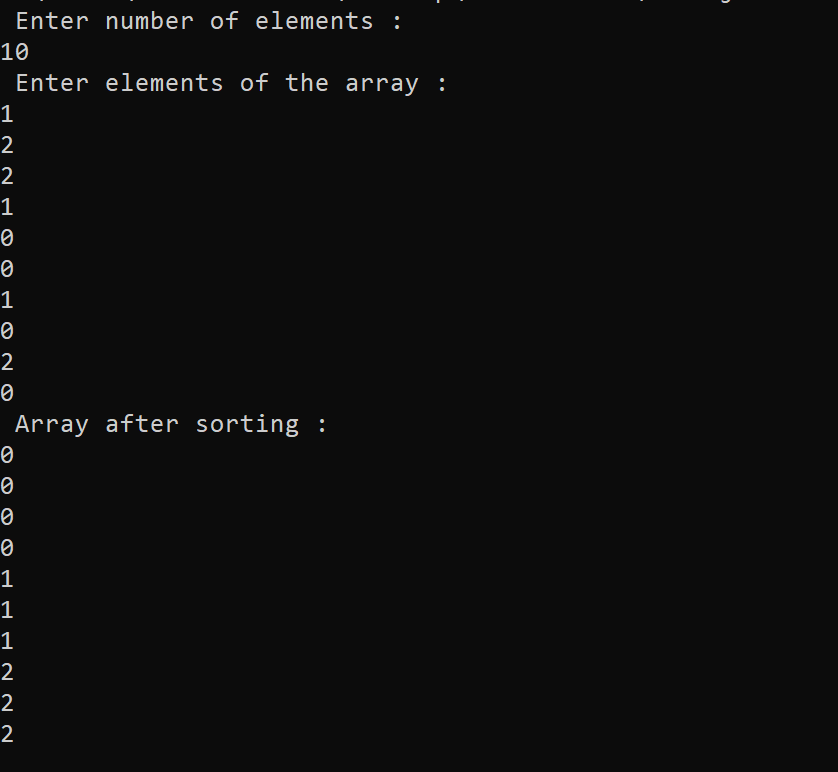

Program of sorting of an array containing 0's,1's, and 2's using method 1 in Python Programming Language -

The output of the following Python program for sorting the array of 0's, 1's, and 2's using Method # 2

Program of sorting of an array containing 0's,1's, and 2's using method 2 in Java Programming Language -

The output of the following JAVA program for sorting the array of 0's, 1's, and 2's using Method # 2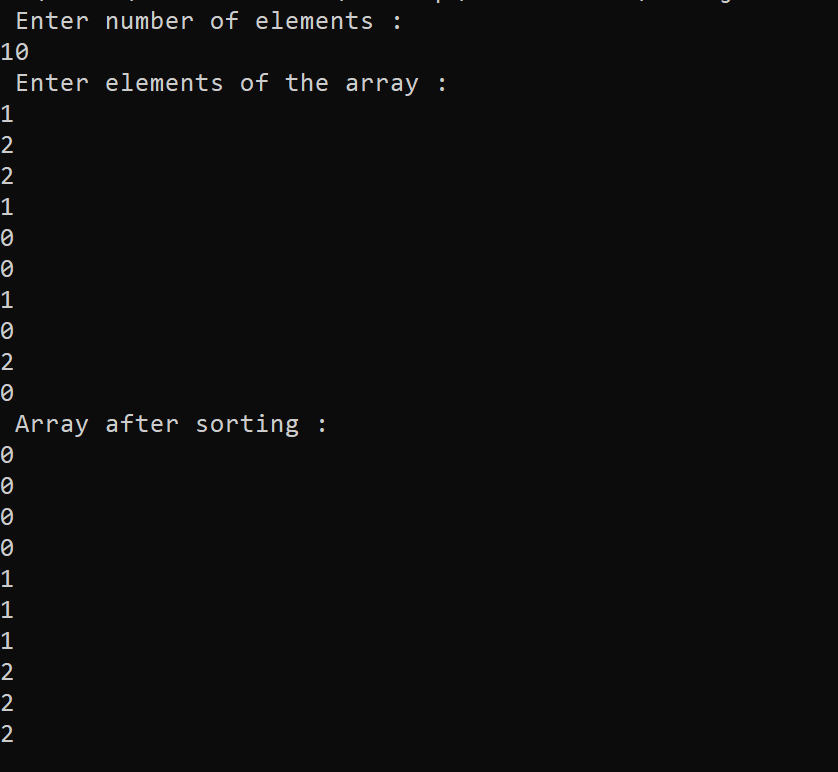

After executing the program successfully in a specific programming language and following the optimized three-way partitioning algorithm using a single traversal approach, we will get the proper result, i.e., sorting an array in ascending order.

Now let us analyze the running time and performance of the algorithm we are applying to sort the array in ascending order by finding the algorithm's time complexity and space complexity using in Method # 1.

Time Complexity of Method # 2 -

For finding the time complexity, we need to observe the algorithm and analyze the time taken by a particular line for execution. We can observe that we require traversing the array only once for comparing the value present at index mid with 0, 1, and 2. We will apply the necessary operations regarding the above conditions. After traversal is done, we will get the sorted array as a result. Hence time complexity will be -

T ( n ) = C + O ( n )

T ( n ) = O ( n )

Here ' C ' be any constant time taken for swapping and assigning the values in the variable.

Hence time complexity will be O ( n ), as we do the asymptotically rough idea that we require ' n ' time to solve the problem of ' n ' elements.

Space Complexity of Method # 2 -

To find space complexity, we need to observe the program and analyze the space required to store all the variables; as we notice the program, we will observe that no extra space is required to store the elements.

S ( n ) = O ( 1 )

Hence the space complexity for above method # 2 will be constant.