Counting Beautiful Numbers in a Specified Range
Problem Statement
A positive integer is considered Beautiful if it satisfies two criteria:
The quantity of even digits in the number matches the count of odd digits.
The number is evenly divisible by a given integer k.
Our task is to calculate and return the total count of Beautiful numbers within the inclusive range [low, high].
Java Approach 1 Using Brute Force
Output:
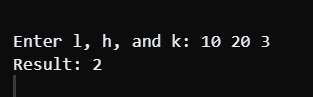
Code Explanation:
- The code defines a Java class that counts "beautiful integers" within a specified range [l, h] with a given step k. The help method iterates through the range for different powers of 10, counting integers where the number of even and odd digits is equal. The numberOfBeautifulIntegers method calculates the total count by invoking help for specific powers of 10.
- A special case optimizes the result for certain input values. The main Method takes user input for the range and step and then displays the computed count.
Time Complexity:
- The time complexity of the numberOfBeautifulIntegers method is O((h - l) * log(h)), dominated by the nested loops iterating over the range of numbers and their digits.
Space Complexity:
- The space complexity is O(1) as the algorithm uses a constant amount of extra space, mainly for iteration and counting variables, regardless of the input size.
- The help method contributes to the overall time complexity, and the primary space complexity arises from input and output variables.
Java Approach 2 Using Dynamic Programming
Output:
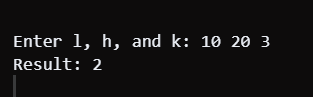
Code Explanation:
The code calculates the count of "beautiful integers" within a given range [low, high] with a specified step k. It uses dynamic programming and recursion. The recursive function f explores all possible combinations of digits, considering constraints such as parity. Memoization optimizes the process by storing previously computed results. The Method numberOfBeautifulIntegers initializes the calculation for the lower and upper bounds, subtracting the results to obtain the count within the specified range. The logic involves:
- Iterating through the digits of the numbers.
- Updating counts based on conditions.
- Efficiently storing and retrieving intermediate results to improve overall efficiency.
Time Complexity:
- The The recursion involves a loop that runs up to the maximum digit value (up to 9). Therefore, the time complexity is O(N * D * 10 * 21 * 21), where N is the number of digits in the input range, and D is the maximum digit value (10 digits)..
Space Complexity:
- The space complexity is determined by the storage required for the memoization table dp. The memoization table has dimensions based on the length of the input numbers and additional factors related to the state of the recursive function.
- The space complexity is O(N * 2 * 2 * 21 * 21), where N is the length of the input numbers.
Java Approach 3 Using Divide And Conquer
Output:
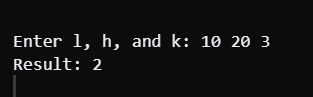
Code Explanation:
- The divide-and-conquer approach breaks the problem of counting beautiful integers into subproblems by recursively dividing the input range. The algorithm calculates the count of beautiful integers for the left and right halves, combining the results. It leverages digit-wise processing, calculating the range for each digit.
- The base case handles single-digit numbers, and a helper function efficiently computes powers of 10. By dividing the range and conquering subproblems, the algorithm reduces complexity and optimizes computation. The recursive structure efficiently explores the entire range, counting beautiful integers.
Time Complexity:
- The divide-and-conquer algorithm's time complexity is O(log(high)) as it recursively divides the range by digit, and each level corresponds to a digit in the input numbers.
Space Complexity:
The space complexity is O(log(high)) due to the recursive call stack, where each level represents the processing of a digit. The algorithm maintains a minimal amount of additional space, mainly for variables and intermediate calculations.
|
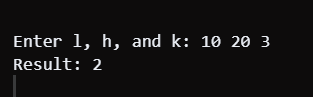
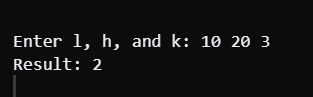
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









