DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Closest greater or same value on left side for every element in arrayGiven an array of integers, our goal is to find, for each element, the closest value on its left side that is greater than or equal to the element itself. In essence, we need to construct a new array where each element corresponds to the closest greater or equal value on the left side of the original array. For example, consider the array: [5, 9, 3, 6, 8]. The new array, following the problem's criteria, would be: [-1, -1, 5, 9, 9]. In this case, for the first element '5', there is no element greater than or equal to it on its left side, so it remains '-1'. The second element '9' has no greater or equal value on its left side, making it '-1'. The third element '3' has the closest greater or equal value '5' on its left side. Similarly, the fourth and fifth elements '6' and '8' have their respective closest greater or equal values on the left. Note: Before looking into the solution, I would highly recommend you to think of an approachBrute Force Approach One straightforward approach to solving this problem is to use a brute force algorithm. For each element in the array, we can iterate through its left side and find the closest greater or equal value. This approach involves nested loops and has a time complexity of O(n^2), where 'n' is the number of elements in the array. While this approach is conceptually simple, it's not suitable for larger arrays due to its inefficiency. Output: 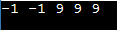
In this approach, for each element at index 'i', we iterate through elements from 'i-1' to '0' and find the closest greater or equal value. This approach has a time complexity of O(n^2), where 'n' is the number of elements in the array. Optimized Approach using Stack To improve the efficiency of our solution, we can utilize a stack-based approach. The idea is to maintain a stack that holds the indices of elements in decreasing order of their values as we traverse the array from left to right. This ensures that the elements in the stack are always greater than or equal to the current element. As we encounter each new element, we can pop elements from the stack until we find a value that's greater than or equal to the current element or until the stack becomes empty. The index of the element at the top of the stack (if any) gives us the closest greater or equal value on the left side for the current element. This approach has a time complexity of O(n) since each element is pushed and popped from the stack only once. The stack size never exceeds the number of elements, and each element is processed exactly once. Output: 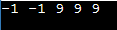
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









