Right View of Binary Tree

The common non-linear data structure known as a tree. A tree illustrates a hierarchical structure in contrast to other data structures such an array, stack, queue, and linked list, which are linear in nature. A tree's ordering information is irrelevant. Two pointers and nodes make up a tree. The parent node's left and right children are represented by these two pointers. Let's thoroughly comprehend the words used in trees.

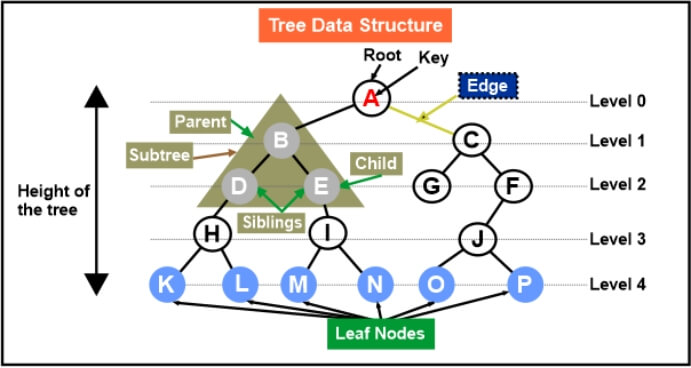
• The highest node in a tree that has no parent nodes is considered the root of the tree. Every tree has a single root node.
• Parent Node: A node's parent one is the node that came before it in the tree of nodes.
• Child Node: The node that is a node's direct successor is referred to as a node's child node.
• Siblings are the children of the same parent node.
• Edge: Edge serves as a connecting node between the parent and child nodes.
• Leaf: A node without children is referred to as a leaf node. It is the tree's last node. A tree may have several leaf nodes.
• A node's subtree is the tree that views that specific node as the root node.
• Depth: The depth of a node is the separation between it and the root node.
• Height: The height of a node is the distance between it and the subtree's deepest node.
• The maximum height of any node is referred to as the tree's height. The height of the root node is the same as this.
• Level: In the tree, a level is the number of parents that correspond to a particular node.
• Node degree: A node's degree is determined by how many children it has.
• A binary tree has (N+1) NULL nodes, where N is the total number of nodes in the tree.

Why use a tree-based data structure?

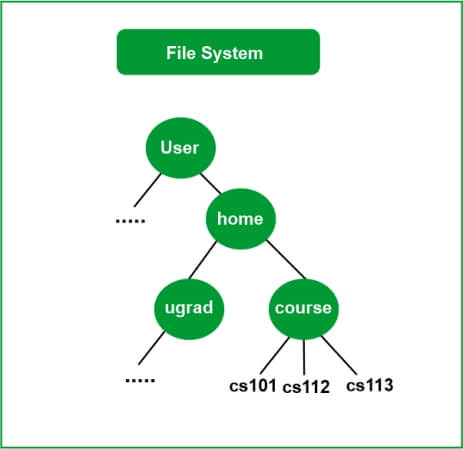
1. You might wish to store information that naturally develops a hierarchy, which is one reason to use trees. For instance, a computer's file system:
   
2. Trees offer reasonable access/search (with some ordering, like BST) (quicker than Linked List and slower than arrays).
3. Trees offer limited insertion and deletion (quicker than Arrays and slower than Unordered Linked Lists).
4. Because pointers are used to connect nodes, trees, like linked lists, have no maximum number of nodes.

The primary uses for tree data structures include:

• Manipulation of data in hierarchies.
• Make information searchable (see tree traversal).
• Manipulate data-sorted lists.
• For the purpose of composing digital pictures for visual effects.
• Routing protocols
• Multi-stage decision-making process type (see business chess).

What is a Binary Tree?

A binary tree is a tree data structure made up of nodes also known as left and right nodes-each of which has a maximum of two offspring. The tree starts at the root node.

Binary Tree Representation

Each node in the tree has the following information:

• Pointer to the left child
• Pointer to the right child

In C, we may use structures to represent a tree node. We may utilise classes as a component of other languages' OOP features. An illustration of a tree node containing integer data is shown below.

A collection of nodes that are visible when a binary tree is viewed from the right side is known as the right view.

Example:

Output:

Right view of the tree is 1 3 7 8

Right View of Binary Tree using Recursion

Utilizing recursion while simultaneously keeping track of the highest level is the notion. Additionally, go through the tree so that the right subtree is encountered before the left subtree.

The application of the aforementioned strategy is seen below:

Output:

1 3 7 8
?????..
Process executed in 1.11 seconds
Press any key to continue.

Explanation

To solve the issue, adhere to the instructions listed below:

• Postorder traversal should be used to retrieve the rightmost node first.
• Maintain a variable called max_level that will hold data up until the correct view is printed.
• If the current level is higher than max_level when traversing the tree in postorder fashion, print the current node and increase max_level by the current level.

Right View of Binary Tree Using Level Order Traversal

Output:

 1 3 7 8 
????
Process executed in 1.22 seconds
Press any key to continue

Explanation

Utilizing Level Order Traversal is the plan since the final node of each level provides the correct perspective of the binary tree.

To solve the issue, adhere to the instructions listed below:

• Traverse the tree in level sequence.
• Print the level's last node for each level.