Islands in a graph using BFS

Introduction

Graphs are basic data structures that show an arrangement of edges and nodes. They are used in many different domains, such as computer networks and social networks. Finding islands within a graph is an intriguing topic in graph theory. When discussing graphs, islands are frequently referred to as connected components or subgraphs in which every node can be reached from every other node.

A graph traversal algorithm called Breadth-First Search investigates every vertex in a graph level by level. Before going on to the next level of vertices, BFS investigates its neighbors starting from a specified source vertex. Because of this feature, BFS is appropriate for tasks such as determining the shortest path between two nodes or identifying linked components within a network. Imagine a situation where a network of connected nodes is represented as a graph. In this context, an island is a collection of nodes that are linked to one another but not to nodes outside the group. In such a graph, we may use BFS to explore and mark related components in order to determine the number of islands.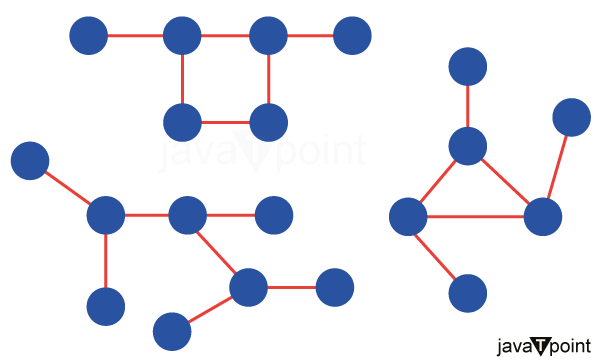

Code

#includ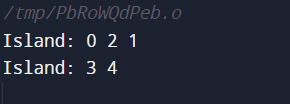e <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_VERTICES 100
struct Node {
    int data;
    struct Node* next;
};
struct Graph {
    int numVertices;
    struct Node** adjacencyList;
};
struct Node* createNode(int data) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}
struct Graph* createGraph(int numVertices) {
    struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
    graph->numVertices = numVertices;
    graph->adjacencyList = (struct Node**)malloc(numVertices * sizeof(struct Node*));
    for (int i = 0; i < numVertices; ++i) {
        graph->adjacencyList[i] = NULL;
    }
    return graph;
}
void addEdge(struct Graph* graph, int src, int dest) {
    struct Node* newNode = createNode(dest);
    newNode->next = graph->adjacencyList[src];
    graph->adjacencyList[src] = newNode;
    newNode = createNode(src);
    newNode->next = graph->adjacencyList[dest];
    graph->adjacencyList[dest] = newNode;
}
void BFS(struct Graph* graph, int startVertex, bool visited[]) {
    int queue[MAX_VERTICES];
    int front = -1, rear = -1;
    queue[++rear] = startVertex;
    visited[startVertex] = true;
    while (front != rear) {
        int currentVertex = queue[++front];
        printf("%d ", currentVertex);
        struct Node* temp = graph->adjacencyList[currentVertex];
        while (temp != NULL) {
            int adjVertex = temp->data;
            if (!visited[adjVertex]) {
                queue[++rear] = adjVertex;
                visited[adjVertex] = true;
            }
            temp = temp->next;
        }
    }
}
int main() {
    struct Graph* graph = createGraph(5);
    addEdge(graph, 0, 1);
    addEdge(graph, 0, 2);
    addEdge(graph, 1, 2);
    addEdge(graph, 3, 4);
    bool visited[MAX_VERTICES] = {false};
    for (int i = 0; i < graph->numVertices; ++i) {
        if (!visited[i]) {
            printf("Island: ");
            BFS(graph, i, visited);
            printf("\n");
        }
    }
    return 0;
}

Output:

Code Explanation

Graph Illustration

The graph is represented as an adjacency list in the code. The Graph structure comprises an array of linked lists (adjacencyList) and the number of vertices (numVertices). Each element of the array represents a vertex, and the linked list that corresponds to it records the vertices that are adjacent to it.

Node Creation

The Node structure represents a node in the linked list. The task of establishing a new node with a specified data value falls to the createNode function.

Graph Development

A new graph is initialized with a predetermined number of vertices using the createGraph function. The graph structure's memory is allocated, and NULL pointers are used to initialize the adjacency list.

Edge Addition

An undirected edge is added to the graph between two vertices via the addEdge function. It updates the adjacency lists by generating new nodes at the source and destination vertices.

Breadth-First Search (BFS)

The BFS function starts at a specified vertex (startVertex) and traverses the BFS. It searches neighboring vertices level by level and keeps track of visited vertices using a queue. The First In First Out (FIFO) principle directs the traversal.

Main Function

A graph with five vertices is constructed in the main function, and edges are added to show the connections between the vertices. To keep track of whether a vertex has been visited during BFS, utilize the visited array.

Identification of the Island

Subsequently, the primary function traverses all vertices and executes BFS on every unexplored vertex. The vertices are printed for each connected component (island) that is found in the order that they are visited during BFS.

Time and Space Complexity

The Breadth-First Search (BFS) algorithm affects the time complexity of the given C code. In the worst-case scenario, when all vertices and edges are explored, the time complexity is O(V + E), where V is the number of vertices and E is the number of edges. This is because BFS traverses each vertex and edge once. In the code's specific example, where the number of vertices is denoted by V and the number of edges is denoted by E, the time complexity can be regarded as O(V + E).

The data structures that are utilized to implement BFS and describe the graph largely dictate the space complexity. O(V + E) space is needed for the graph's adjacency list representation, where V denotes the number of vertices and E is the number of edges. The BFS queue, which, in the worst-case scenario, might have a maximum size of V, is the source of the extra space complexity. Because of the space needed for the BFS traversal and the graph representation, the code's overall space complexity is O(V + E).

Next TopicIterative Letter Combinations of a Phone Number

← prev next →