Inorder Tree Traversal without Stack

In any data structure, traversal is an important operation. In the traversal operation, we walk through each element of the data structure at least once. The traversal operation plays a very important role in various other operations on the data structure like searching. We need to visit each element of the data structure atleast once to compare each incoming element to the key that we want to find in the data structure.

Like any other data structure, the tree data also needs to be traversed to access each element, known as a node of the tree data structure. There are different ways of traversing a tree depending upon the order in which the tree's nodes are visited and the types of data structure used for traversing the tree.

There are various data structures involved in traversing a tree, as traversing a tree involves iterating over all nodes in some manner. As from a given node, there could be more than one way to traverse or visit the next node of the tree, so it becomes important to store one of the nodes traverses further and store the rest of the nodes having a possible path for backtracking the tree if needed.

As we know, backtracking is not a linear approach, so we need different data structures for traversing through the whole tree.

Types of Tree Traversal

The stack and queue are the major data structure that is used for traversing a tree. So depending upon the order in which the nodes of the tree are visited, the different types of tree traversal are:

Depth First Search Tree Traversal
- Pre-order Tree Traversal.
- Post-order Tree Traversal.
- In-order Tree Traversal.
- Reverse Pre-order Tree Traversal.
- Reverse Post-order Tree Traversal.
- Reverse In-order Tree Traversal.
Breadth-First Search tree Traversal.

Now, we will be focusing on the in-order tree traversal type. All three types; in-order tree traversal, pre-order tree traversal and post-order tree traversal, have the difference of visiting the tree's root node, such as:

In pre-order tree traversal, the tree's root node is visited first, followed by the left node (or subtree) and right node (or subtree).
In in-order tree traversal, the left node (or subtree) is visited first, followed by the root node and then the right node (or subtree).
And in the post-order tree traversal, the left node (or subtree) is visited first, followed by the right node (or subtree) and the root node of the tree is visited in the last.

In-order Tree Traversal

In-order traversal can be defined as the traversal that will process all tree nodes by recursively processing the left subtree, then processing the root, and finally the right subtree.

For example, let us write an in-order traversal for the tree given below.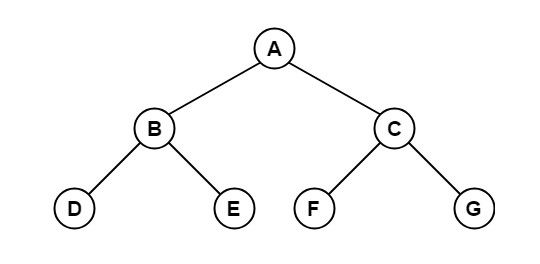

The above tree has seven nodes in it. Node A is the tree's root node, having three nodes in its left and right subtrees, respectively.

According to the in-order tree traversal definition, the left subtree should be visited first, and in the left subtree, the deepest left node is node D.
Then the root of this subtree is visited node B (the left subtree's root node).
In the last, the rightmost node of the binary tree, node E, is visited, so now our left subtree is completed traversed, we will visit the root node A, and in the last, the right subtree is traversed.
Similarly, in the right subtree, we first need to traverse the leftmost node, node F and then visit the root node of the right subtree, node C. In the end, the rightmost node of the right subtree is visited that is node G.
So, the in-order tree traversal of the above tree is:

The stack data structure is mostly used for the in-order traversal of a tree, but in this article, we will see the recursive way to traverse the tree.

C++ Code:

Let's write a C++ code for in-order tree traversal of the tree using recursion.

// A sample C++ Code to create a tree and in-order traverse the tree 

// The iostream library is used to use the console to get and print the data from the user 
#include <iostream>
using namespace std;
 
// A struct named node is created that will act as a single node of the binary tree 
struct Node
{

    // a variable named data of integer type is created that will hold the data that is present in that particular node of the complete binary tree
    int data;
    

    // two variables named right and left of the node type are created that will be used to hold the addresses of the right child node and the left child node of a parent node present on the complete binary tree
    Node *left, *right;
 

    // A constructor of the struct named Node is written that will have one parameter of integer type that will set its value to the data variable of the struct 
    Node(int data)
    {
        this->data = data;
        this->left = this->right = nullptr;
    }
};//end of Node struct
 
// Recursive function to perform in-order traversal on the tree

/*
* A Recursive function named in the order is written to traverse the tree in an inorder fashion
* This Recursive function will be called for each of the subtrees of the whole tree
* In each subtree, according to the definition of the in-order tree traversal, this function will first print the leftmost leaf child node of the tree
* After printing the leftmost leaf child node, it will print the root node of the tree, and then in the last, the rightmost child leaf node is printed, and it is called again for another subtree 
*/
void inorder(Node* root)
{
    // return if the current node is empty
    if (root == nullptr) {
        return;
    }
 
    // This will Traverse the left subtree and print the nodes of the tree according to the definition of the in order tree traversal 
    inorder(root->left);
 
    // Display the data part of the root (or current node)
    cout << root->data << " ";
 
    // This will Traverse the right subtree and print the nodes of the tree according to the definition of the in order tree traversal 
    inorder(root->right);
}
 

 // A main() function is written to create tree and in-order traverse the tree 
int main()
{
    /* Construct the tree shown below in the comments
               10
             /   \
            /     \
           20       30
          /      /   \
         /      /     \
        40      50       60
              / \
             /   \
            70     80
    */
 
// An object named root of the struct named Node is created that will act as a root node of the tree having value 10 
    Node* root = new Node(10);
    
    // add left and right child nodes to the root node of the tree having values 20 and 30 respectively
    root->left = new Node(20);
    root->right = new Node(30);

    // add left child node to the left node of the root node of the tree having value 40
    root->left->left = new Node(40);
    
    // add left and right child nodes to the right node of the root node of the tree having values 50 and 60 respectively
    root->right->left = new Node(50);
    root->right->right = new Node(60);

    // add left and right child nodes to the left node of the right node of the root node of the tree having values 70 and 80 respectively
    root->right->left->left = new Node(70);
    root->right->left->right = new Node(80);

    /*
    * Once the tree is created, and all the nodes of the tree are assigned their values, the inorder function 
    * the root of the tree is passed as a parameter to the inorder function
    */

    cout<<"The inorder traversal of the tree with recusion is ::";
    cout<<endl;
    inorder(root);
    
    cout<<endl;
    return 0;
}//end of the main fucntion

Output: The output of the above code is:

The inorder traversal of the tree with recursion is:
40 20 10 70 50 80 30 60

In the above C++ code, we have used recursion instead of the stack data structure to traverse the tree. For the traversal of the tree, a recursive function named 'inorder' is created that will be called recursively to traverse through the tree. This recursive function will be called for each of the subtrees of the whole tree.

In each subtree, this function will first print the leftmost leaf child node of the tree. After printing the leftmost leaf child node, it will print the tree's root node, and then in the last, the rightmost child leaf node is printed and called again for another subtree. So, all tree nodes are traversed successfully by giving recursive calls to the inorder() function.

Java Code:

Now let's write a code in Java to create a tree and print the elements of the tree in the in-order tree traversal manner.

// A sample Java Code to create a tree and in-order traverse the tree 


// A class named node is created that will act as a single node of the binary tree 
class Node
{
    // a variable named data of integer type is created that will hold the data that is present in that particular node of the complete binary tree
    int data;
    
    // two variables named right and left of the node type are created that will be used to hold the addresses of the right child node and the left child node of a parent node present on the complete binary tree
    Node left, right;
 
    // A constructor of the struct named Node is written that will have one parameter of integer type that will set its value to the data variable of the struct
    public Node(int key)
    {
        data = key;
        left = right = null;
    }
}//end of the Node class
 


// A class named Main is written to create the tree and in-order traverse the tree
class Main
{
   // / Recursive function to perform inorder traversal on the tree

/*
* A Recursive function named in the order is written to traverse the tree in an inorder fashion
* This Recursive function will be called for each of the subtrees of the whole tree
* In each subtree, according to the definition of the in-order tree traversal, this function will first print the leftmost leaf child node of the tree
* After printing the leftmost leaf child node, it will print the root node of the tree, and then in the last, the rightmost child leaf node is printed, and it is called again for another subtree 
*/
    public static void inorder(Node root)
    {
        // return if the current node is empty
        if (root == null) {
            return;
        }
    
        // This will Traverse the left subtree and print the nodes of the tree according to the definition of the in order tree traversal 
        inorder(root.left);
    
        // Display the data part of the root (or current node)
        System.out.print(root.data + " ");
    
        // This will Traverse the right subtree and print the nodes of the tree according to the definition of the in order tree traversal 
        inorder(root.right);
    }
 

     // A main() function is written to create tree and in-order traverse the tree 
    public static void main(String[] args)
    {
        
    /* Construct the tree shown below in the comments
               10
             /   \
            /     \
           20       30
          /      /   \
         /      /     \
        40      50       60
              / \
             /   \
            70     80
    */
 

        // An object named root of the struct named Node is created that will act as a root node of the tree having value 10 
        Node root = new Node(10);

        // add left and right child nodes to the root node of the tree having values 20 and 30 respectively
        root.left = new Node(20);
        root.right = new Node(30);

        // add left child node to the left node of the root node of the tree having value 40
        root.left.left = new Node(40);

        // add left and right child nodes to the right node of the root node of the tree having values 50 and 60 respectively
        root.right.left = new Node(50);
        root.right.right = new Node(60);

        // add left and right child nodes to the left node of the right node of the root node of the tree having values 70 and 80 respectively
        root.right.left.left = new Node(70);
        root.right.left.right = new Node(80);
 
        /*
        * Once the tree is created, and all the nodes of the tree are assigned their values, the inorder function 
        * the root of the tree is passed as a parameter to the inorder function
        */
        
        System.out.println("The inorder traversal of the tree with recusion is ::");
        inorder(root);
        System.out.println();
    }
}//end of the Main Class

Output: The output of the above code is:

The inorder traversal of the tree with recursion is:
40 20 10 70 50 80 30 60

In the above Java code, we have used recursion instead of the stack data structure to traverse the tree. For the traversal of the tree, a recursive function named 'inorder' is created that will be called recursively to traverse through the tree. This recursive function will be called for each of the subtrees of the whole tree.

In each subtree, according to the definition of the in-order tree traversal, this function will first print the leftmost leaf child node of the tree. After printing the leftmost leaf child node, it will print the tree's root node, and then in the last, the rightmost child leaf node is printed and called again for another subtree. So, all tree nodes are traversed successfully by giving recursive calls to the inorder() function.

Next TopicEnumeration of Binary Trees

← prev next →