Suffix Trees in data structure
Introduction to Suffix Tree
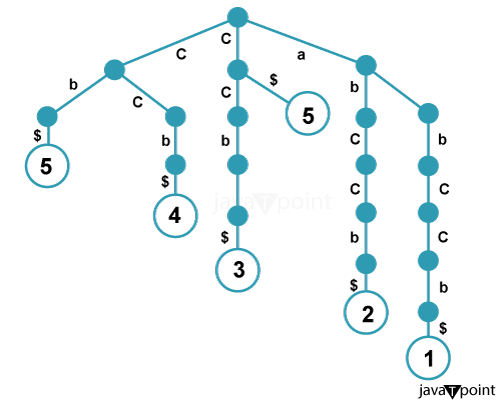
In the domain of data structures, we encounter the entity known as a "suffix tree." This complicated construct finds its purpose to guard a collection of strings. In this case, the unique suffixes within the merge, converging into a solitary node or main branch within this complicated cluster.
Although there are many different approaches to building a suffix tree, most suffix trees, if not all of them, share the following semantics:
- Every substring has an additional special character added to it.
- The index or starting position of the suffix that each leaf node represents is contained in it.
- Each suffix's alphabets are condensed into a single node representation.
It's critical to understand the distinction between a trie and a suffix tree before learning about suffix trees.
Trie
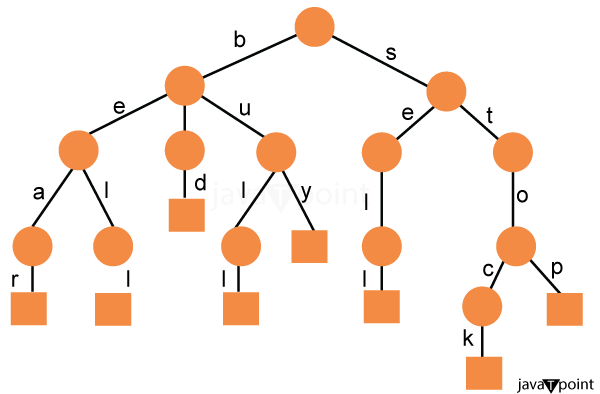
In the domain of data structures, a "trie" unfolds its complicacy as it secretly separates each character of all the strings within its designated array. This careful selection, denoted by the presence of individual nodes, sets it apart from conventional structures. When a common sub-string commences multiple words, a unifying chain of nodes emerges to encapsulate this shared linguistic fragment.
The chain gracefully disbands where the sub-string concludes, gracefully giving way to the inception of unique suffixes. Consequently, each character of these distinctive suffixes finds its representation through the discrete and specialized nodes that constitute the trie's complicated fabric.
Functionality of Suffix Tree
In the event that the symbols stem from an integer alphabet encompassing a polynomial range extending from negative infinity to positive infinity, then the construction of a suffix tree for a string denoted as 'S' with a length denoted as 'n' can be accomplished in a time complexity of Theta (n). This particularly holds true when dealing with alphabets of fixed dimensions. However, for more expansive alphabets, a considerable portion of the temporal resources is allocated to the task of organizing the symbols into a range of size O(n), a procedure that typically demands O(nlog n) time.
Assuming the existence of a suffix tree erected over the string 'S' with a length of 'n', several operations can be performed:
1. Searching for character sequences: -
- In a timeframe of O(m), one can ascertain whether a character sequence labeled as 'P' with a length of 'm' qualifies as a substring.
- In a timeframe of O(m), it is feasible to identify the initial appearance of sequences 'P1...PQ' whose cumulative length amounts to 'm' as substrings.
- In a timeframe of O(m+z), one can pinpoint all 'z' occurrences of the patterns 'P1...PQ' with a length of 'm' within substrings.
2. Discerning characteristics of the character sequences: -
- In a timeframe of Theta(n(i) + n(j)), the most extensive common substrings shared between the character strings 'S(i)' and 'S(j)' can be determined.
- In a timeframe of Theta (n + z), all maximal pairings, maximal repeats, and super maximal repeats can be unveiled.
- In a timeframe of Theta (n), the lengthiest recurring substrings can be identified.
- In a timeframe of Theta (n), the substrings of minimum length that occur solely once can be discerned.
Applications of Suffix Tree
Additionally, suffix trees can be applied to a broad range of string challenges in bioinformatics, editing, and free-text search, among other applications. Following is a list of some of the most popular uses:
- Precise String Correspondence: As previously concluded, within the suffix tree of the given text, the entirety of pattern P's occurrences may be unearthed in a time complexity of O (P + occ). Even when considering the temporal investment in constructing the suffix tree, this approach asymptotically rivals the efficiency of Knuth-Morris-Pratt, especially when dealing with multiple patterns.
- Computational Genomics: Suffix trees find prevalent application in the domain of Bioinformatics, specifically for the identification of recurring motifs within a DNA strand. Moreover, they are invaluable for the revelation of the longest common sub-string or sub-sequence within a DNA sequence. Such techniques hold paramount importance in the domains of evolutionary biology and the discernment of shared genetic features among organisms.
- Textual Metrics: Each node in the suffix tree corresponds distinctly to a textual factor, and conversely, each factor correlates with a unique node. Consequently, even though the yielded value traditionally adheres to Theta(n^2), the total assortment of diverse factors within the text equates to the number of distinctive nodes, a quantity that can be computed in linear time, O(n), by systematically traversing the suffix tree. The longest recurrent factor within the text signifies the most extended sequence that recurs at least twice, which is succinctly represented by the innermost node of the suffix tree.
- Supreme Palindromic Sequences: A palindrome epitomizes a sequence that remains unaltered when reversed, as exemplified by the word "racecar." This concept within the domain of suffix trees serves as a valuable tool for discerning the most extended palindromic sequences.
- Data Reduction Strategies: Data compression, in the field of signal processing, encapsulates the art of encoding information using fewer bits than its initial representation.
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









