What is a Trie data structure?

The word "Trie" is an excerpt from the word "retrieval". Trie is a sorted tree-based data-structure that stores the set of strings. It has the number of pointers equal to the number of characters of the alphabet in each node. It can search a word in the dictionary with the help of the word's prefix. For example, if we assume that all strings are formed from the letters 'a' to 'z' in the English alphabet, each trie node can have a maximum of 26 points.

Trie is also known as the digital tree or prefix tree. The position of a node in the Trie determines the key with which that node is connected.

Properties of the Trie for a set of the string:

The root node of the trie always represents the null node.
Each child of nodes is sorted alphabetically.
Each node can have a maximum of 26 children (A to Z).
Each node (except the root) can store one letter of the alphabet.

The diagram below depicts a trie representation for the bell, bear, bore, bat, ball, stop, stock, and stack.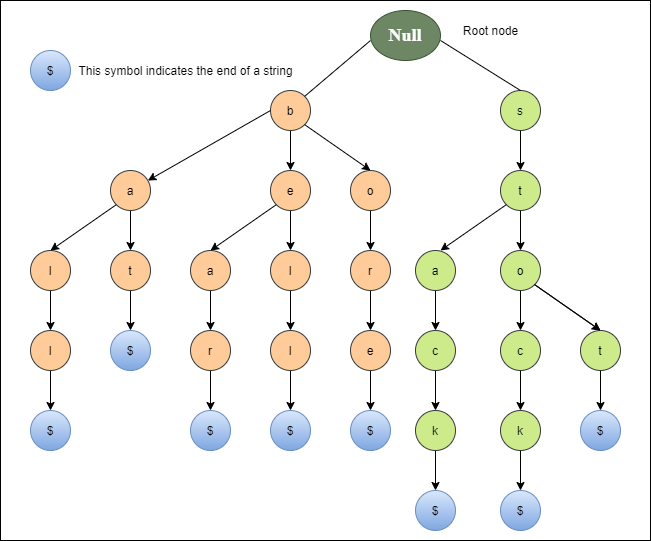

Basic operations of Trie

There are three operations in the Trie:

Insertion of a node
Searching a node
Deletion of a node

Insert of a node in the Trie

The first operation is to insert a new node into the trie. Before we start the implementation, it is important to understand some points:

Every letter of the input key (word) is inserted as an individual in the Trie_node. Note that children point to the next level of Trie nodes.
The key character array acts as an index of children.
If the present node already has a reference to the present letter, set the present node to that referenced node. Otherwise, create a new node, set the letter to be equal to the present letter, and even start the present node with this new node.
The character length determines the depth of the trie.

Implementation of insert a new node in the Trie

public class Data_Trie {
    private Node_Trie root;
    public Data_Trie(){
        this.root = new Node_Trie();
    }
    public void insert(String word){
        Node_Trie current = root;
        int length = word.length();
        for (int x = 0; x < length; x++){
            char L = word.charAt(x);
            Node_Trie node = current.getNode().get(L);
            if (node == null){
                node = new Node_Trie ();
                current.getNode().put(L, node);
            }
            current = node;
        }
        current.setWord(true);
    }
}

Searching a node in Trie

The second operation is to search for a node in a Trie. The searching operation is similar to the insertion operation. The search operation is used to search a key in the trie. The implementation of the searching operation is shown below.

Implementation of search a node in the Trie

class Search_Trie {

    private Node_Trie Prefix_Search(String W) {
        Node_Trie node = R;
        for (int x = 0; x < W.length(); x++) {
           char curLetter = W.charAt(x);
           if (node.containsKey(curLetter)) 
             {
               node = node.get(curLetter);
              } 
           else {
               return null;
           }
        }
        return node;
    }

    public boolean search(String W) {
       Node_Trie node = Prefix_Search(W);
       return node != null && node.isEnd();
    }
}

Deletion of a node in the Trie

The Third operation is the deletion of a node in the Trie. Before we begin the implementation, it is important to understand some points:

If the key is not found in the trie, the delete operation will stop and exit it.
If the key is found in the trie, delete it from the trie.

Implementation of delete a node in the Trie

public void Node_delete(String W) 
{
    Node_delete(R, W, 0);
}
 
private boolean Node_delete(Node_Trie current, String W, int Node_index) {
    if (Node_index == W.length()) {
        if (!current.isEndOfWord()) {
            return false;
        }
        current.setEndOfWord(false);
        return current.getChildren().isEmpty();
    }
    char A = W.charAt(Node_index);
    Node_Trie node = current.getChildren().get(A);
    if (node == null) {
        return false;
    }
    boolean Current_Node_Delete = Node_delete(node, W, Node_index + 1) && !node.isEndOfWord();
 
    if (Current_Node_Delete) {
        current.getChildren().remove(A);
        return current.getChildren().isEmpty();
    }
    return false;
}

Applications of Trie

1. Spell Checker

Spell checking is a three-step process. First, look for that word in a dictionary, generate possible suggestions, and then sort the suggestion words with the desired word at the top.

Trie is used to store the word in dictionaries. The spell checker can easily be applied in the most efficient way by searching for words on a data structure. Using trie not only makes it easy to see the word in the dictionary, but it is also simple to build an algorithm to include a collection of relevant words or suggestions.

2. Auto-complete

Auto-complete functionality is widely used on text editors, mobile applications, and the Internet. It provides a simple way to find an alternative word to complete the word for the following reasons.

It provides an alphabetical filter of entries by the key of the node.
We trace pointers only to get the node that represents the string entered by the user.
As soon as you start typing, it tries to complete your input.

3. Browser history

It is also used to complete the URL in the browser. The browser keeps a history of the URLs of the websites you've visited.

Advantages of Trie

It can be insert faster and search the string than hash tables and binary search trees.
It provides an alphabetical filter of entries by the key of the node.

Disadvantages of Trie

It requires more memory to store the strings.
It is slower than the hash table.

Complete program in C++

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 26
 
typedef struct TrieNode TrieNode;
 
struct TrieNode {
    char info; 
    TrieNode* child[N];
    int data;
};
 
TrieNode* trie_make(char info) {
    TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
    for (int i = 0; i < N; i++)
        node → child[i] = NULL;
    node → data = 0;
    node → info = info;
    return node;
}
 
void free_trienode(TrieNode* node) {
    for(int i = 0; i < N; i++) {
        if (node → child[i] != NULL) {
            free_trienode(node → child[i]);
        }
        else {
            continue;
        }
    }
    free(node);
}
 
// Trie node loop start
TrieNode* trie_insert(TrieNode* flag, char* word) {
    TrieNode* temp = flag;
     for (int i = 0; word[i] != '\0'; i++) {
       int idx = (int) word[i] - 'a';
        if (temp → child[idx] == NULL) {
            temp → child[idx] = trie_make(word[i]);
        }
        else {
        }
        temp = temp → child[idx];
    }trie
    temp → data = 1;
    return flag;
}
 
int search_trie(TrieNode* flag, char* word)
{
    TrieNode* temp = flag;
 
    for(int i = 0; word[i] != '\0'; i++)
    {
        int position = word[i] - 'a';
        if (temp → child[position] == NULL)
            return 0;
        temp = temp → child[position];
    }
    if (temp != NULL && temp → data == 1)
        return 1;
    return 0;
}
 
int check_divergence(TrieNode* flag, char* word) {
    TrieNode* temp = flag;
    int len = strlen(word);
    if (len == 0)
        return 0;
    int last_index = 0;
    for (int i = 0; i < len; i++) {
        int position = word[i] - 'a';
        if (temp → child[position]) {
            for (int j = 0; j < N; j++) {
                if (j != position && temp → child[j]) {
                    last_index = i + 1;
                    break;
                }
            }
            temp = temp → child[position];
        }
    }
    return last_index;
}
 
char* find_longest_prefix(TrieNode* flag, char* word) {
    if (!word || word[0] == '\0')
        return NULL;
    int len = strlen(word);

    char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
    for (int i = 0; word[i] != '\0'; i++)
        longest_prefix[i] = word[i];
    longest_prefix[len] = '\0';
 
    int branch_idx  = check_divergence(flag, longest_prefix) - 1;
    if (branch_idx >= 0) {
        longest_prefix[branch_idx] = '\0';
        longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
    }
 
    return longest_prefix;
}
 
int data_node(TrieNode* flag, char* word) {
    TrieNode* temp = flag;
    for (int i = 0; word[i]; i++) {
        int position = (int) word[i] - 'a';
        if (temp → child[position]) {
            temp = temp → child[position];
        }
    }
    return temp → data;
}
 
TrieNode* trie_delete(TrieNode* flag, char* word) {
    if (!flag)
        return NULL;
    if (!word || word[0] == '\0')
        return flag;
    if (!data_node(flag, word)) {
        return flag;
    }
    TrieNode* temp = flag;
    char* longest_prefix = find_longest_prefix(flag, word);
    if (longest_prefix[0] == '\0') {
        free(longest_prefix);
        return flag;
    }
    int i;
    for (i = 0; longest_prefix[i] != '\0'; i++) {
        int position = (int) longest_prefix[i] - 'a';
        if (temp → child[position] != NULL) {
            temp = temp → child[position];
        }
        else {
            free(longest_prefix);
            return flag;
        }
    }
    int len = strlen(word);
    for (; i < len; i++) {
        int position = (int) word[i] - 'a';
        if (temp → child[position]) {
            TrieNode* rm_node = temp→child[position];
            temp → child[position] = NULL;
            free_trienode(rm_node);
        }
    }
    free(longest_prefix);
    return flag;
}
 
void print_trie(TrieNode* flag) {
    if (!flag)
        return;
    TrieNode* temp = flag;
    printf("%c → ", temp→info);
    for (int i = 0; i < N; i++) {
        print_trie(temp → child[i]); 
    }
}
 
void search(TrieNode* flag, char* word) {
    printf("Search the word %s: ", word);
    if (search_trie(flag, word) == 0)
        printf("Not Found\n");
    else
        printf("Found!\n");
}
 
int main() {
    TrieNode* flag = trie_make('\0');
    flag = trie_insert(flag, "oh");
    flag = trie_insert(flag, "way");
    flag = trie_insert(flag, "bag");
    flag = trie_insert(flag, "can");
    search(flag, "ohh");
    search(flag, "bag");
    search(flag, "can");
    search(flag, "ways");
    search(flag, "way");
    print_trie(flag);
    printf("\n");
    flag = trie_delete(flag, "oh");
    printf("deleting the word 'hello'...\n");
    print_trie(flag);
    printf("\n");
    flag = trie_delete(flag, "can");
    printf("deleting the word 'can'...\n");
    print_trie(flag);
    printf("\n");
    free_trienode(flag);
    return 0;
}

Output

Search the word ohh: Not Found
Search the word bag: Found!
Search the word can: Found!
Search the word ways: Not Found
Search the word way: Found!
 → h → e → l → l → o → w → a → y → i → t → e → a → b → a → g → c → a → n
deleting the word 'hello'...
 → w → a → y → h → i → t → e → a → b → a → g → c → a → n
deleting the word 'can'...
 → w → a → y → h → i → t → e → a → b → a → g

Next TopicHeap Data Structure

← prev next →