Stack Operations in Data Structure

What is a Stack?

The Last-In-First-Out (LIFO) concept is used by Stacks, a type of linear data structure. The Queue has two endpoints, but the Stack only has one (front and rear). It only has one pointer, top pointer, which points to the stack's topmost member. When an element is added to the stack, it is always added to the top, and it can only be removed from the stack. To put it another way, a stack is a container that allows insertion and deletion from the end known as the stack's top.

LIFO (Last in First out) Method

According to this method, the piece that was added last will appear first. As an actual illustration, consider a stack of dishes stacked on top of one another. We may claim that the plate we put last comes out first because the plate we put last is on top and we take the plate at the top.

Due to the possibility of understating inventory value, LIFO is not a reliable indicator of ending inventory value. Due to increasing COGS, LIFO leads to reduced net income (and taxes). However, under LIFO during inflation, there are fewer inventory write-downs. Results from average cost are in the middle of FIFO and LIFO.

Real Life Example of LIFO

Let's say that business A sells 10 widgets. $100 per, the first five widgets were delivered two days ago. The remaining five widgets, which cost $200 apiece, just got here yesterday. The last items received are the first to go out on the market, according to the LIFO technique of inventory management. How much may the accountant put down as a cost even though seven widgets were sold?

Although the income from each widget is the same because of its fixed sales price, the cost of each widget is determined by the inventory method used. The last item received is the first item sold according to the LIFO mechanism. Accordingly, the $200 widgets were the first to sell. Following that, the business sold two more of the $100 widgets. Five widgets are priced at $200 each, and two are priced at $100, for a total cost of $1,200 for the widgets using the LIFO approach. As opposed to FIFO, which sells the $200 widgets last, the $100 widgets are sold first. As a result, the price of the sold widgets, which breaks down to five at $100 and two at $200, will be reported as $900. That's why LIFO generates bigger profits during price-increasing periods.

Because of this, LIFO increases expenses during times of price growth and decreases net revenue, which also lowers taxable income. Similar to this, LIFO reduces expenses and raises net income during periods of declining prices, which also raises taxable revenue.

Operations on Stack

Certain actions are made available to us so that we can manipulate a stack.

push() to insert an element into the stack
pop() to remove an element from the stack
top() Returns the top element of the stack.
isEmpty() returns true if stack is empty else false.
size() returns the size of stack.

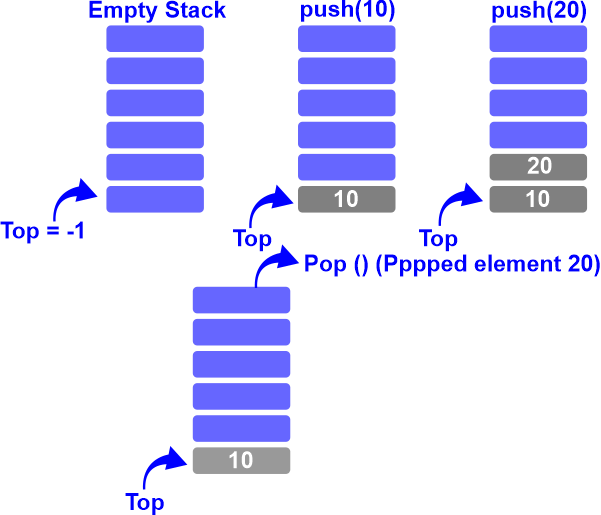
push()

It stacks up a new item. A stack overflow circumstance is when the stack is completely full.

Algorithm for push():

begin
 if stack is full
    return
 endif
else  
 increment top
 stack[top] assign value
end else
end procedure

pop()

It takes something out of the stack. In the opposite sequence from which they were pushed, the things are popped. The condition is referred to as an underflow if the stack is empty.

Algorithm for pop():

begin
 if stack is empty
    return
 endif
else
 store value of stack[top]
 decrement top
 return value
end else
end procedure

top()

It returns the stack's top element.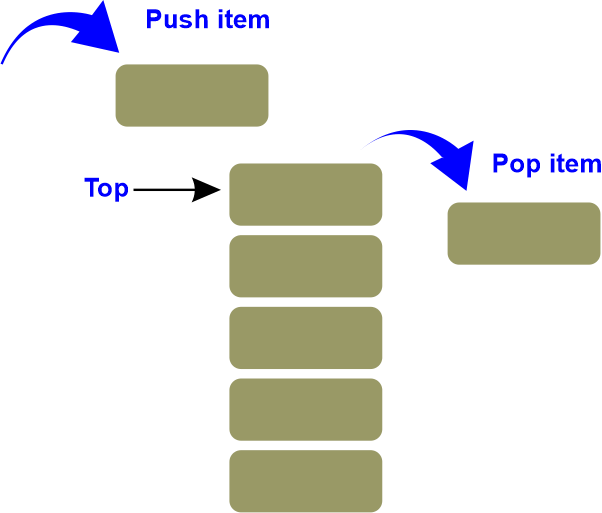

Algorithm for top():

begin 
  return stack[top]
end procedure

isempty()

The answer is true if the stack is empty and false otherwise.

Algorithm for isempty():

begin
 if top < 1
    return true
 else
    return false
end procedure

Practical knowledge about stack

There are several instances of stacks in everyday life. Take the straightforward illustration of dishes stacked on top of one another in a canteen. The plate that is placed at the bottom of the stack stays there for the greatest amount of time since the plate at the top is the first to be taken out. Therefore, it is clear that it adheres to the LIFO/FILO order.

Analysis of Complexity

Operations  	Complexity
push() 	           O(1)
pop()              O(1)
isEmpty()          O(1)
size()	           O(1)

Various Stack Types

Register Stack: The memory unit also has a form of stack called a register that can only handle a tiny amount of data. Because the capacity of the register stack is so little in comparison to the memory, its height is constantly constrained.
Memory Stack: This kind of stack is capable of managing a lot of data from memory. The memory stack can be any height because it uses a lot of memory space.

Some Stack Applications

Conversion from Infix to Postfix or Prefix
There are redo-undo options in numerous locations, including editors like Photoshop.
Web browsers have forward and backward functions.
Utilized in a wide variety of algorithms, including the Tower of Hanoi, tree traversals, stock span issues, and histogram problems.
One of the strategies for constructing algorithms is backtracking. The Knight-Tour issue, N-Queen dilemma, finding your way through a maze, and games like chess or checkers are a few instances of backtracking. In each of these situations, we plunge into a solution, but if that solution is inefficient, we return to the initial state and choose an alternative path. We need a stack in order to save the prior state in order to return from a current state.
Topological Sorting and Strongly Connected Components are two examples of Graph Algorithms
Any modern computer employs a stack as its principal memory management system for conducting operations. A computer system running programs each have their own memory allocations.
Stack can also be used for string reversal. Each character is added into the stack here one by one. Therefore, the initial character of a string is at the bottom of the stack, and its last element is at the top. The stack's pop operations result in a string that is in reverse order.
Computers' implementation of function calls also benefits from stack. The function that was last invoked is always finished first.
Stacks are also employed in text editors to implement the undo/redo function.

Implementing a stack may be done in one of two ways

Using an array
Linking lists

Implementation of Stack using Array:

// C program for array implementation of stack
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>

// A structure to represent a stack
struct Stack {
	int top;
	unsigned capacity;
	int* array;
};

// function to create a stack of given capacity. It initializes size of
// stack as 0
struct Stack* createStack(unsigned capacity)
{
	struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
	stack->capacity = capacity;
	stack->top = -1;
	stack->array = (int*)malloc(stack->capacity * sizeof(int));
	return stack;
}

// Stack is full when top is equal to the last index
int isFull(struct Stack* stack)
{
	return stack->top == stack->capacity - 1;
}

// Stack is empty when top is equal to -1
int isEmpty(struct Stack* stack)
{
	return stack->top == -1;
}

// Function to add an item to stack. It increases top by 1
void push(struct Stack* stack, int item)
{
	if (isFull(stack))
		return;
	stack->array[++stack->top] = item;
	printf("%d pushed to stack\n", item);
}

// Function to remove an item from stack. It decreases top by 1
int pop(struct Stack* stack)
{
	if (isEmpty(stack))
		return INT_MIN;
	return stack->array[stack->top--];
}

// Function to return the top from stack without removing it
int peek(struct Stack* stack)
{
	if (isEmpty(stack))
		return INT_MIN;
	return stack->array[stack->top];
}

// Driver program to test above functions
int main()
{
	struct Stack* stack = createStack(100);
	push(stack, 10);
	push(stack, 20);
	push(stack, 30);
	printf("%d popped from stack\n", pop(stack));
	return 0;
}

OUTPUT:

10 pushed into stack
20 pushed into stack
30 pushed into stack
30 Popped from stack
Top element is : 20
Elements present in stack : 20 10
...........................................................
Process executed in 3.22 seconds
Press any key to continue.

Advantages of Implementation of Stack using Array:

Simple to implement
Since pointers are not used, memory is conserved.

Disadvantage of Implementation of Stack using Array:

It doesn't change size in response to requirements as they arise since it is not dynamic. (However, stacks can also expand and contract with array implementation in the case of dynamically sized arrays like vector in C++, list in Python, and ArrayList in Java.)
It is necessary to establish the stack's overall size in advance.

Implementation of Stack using Linked List:

// C program for linked list implementation of stack
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a stack
struct StackNode {
	int data;
	struct StackNode* next;
};

struct StackNode* newNode(int data)
{
	struct StackNode* stackNode =
	(struct StackNode*)
	malloc(sizeof(struct StackNode));
	stackNode->data = data;
	stackNode->next = NULL;
	return stackNode;
}

int isEmpty(struct StackNode* root)
{
	return !root;
}

void push(struct StackNode** root, int data)
{
	struct StackNode* stackNode = newNode(data);
	stackNode->next = *root;
	*root = stackNode;
	printf("%d pushed to stack\n", data);
}

int pop(struct StackNode** root)
{
	if (isEmpty(*root))
		return INT_MIN;
	struct StackNode* temp = *root;
	*root = (*root)->next;
	int popped = temp->data;
	free(temp);

	return popped;
}

int peek(struct StackNode* root)
{
	if (isEmpty(root))
		return INT_MIN;
	return root->data;
}

int main()
{
	struct StackNode* root = NULL;

	push(&root, 10);
	push(&root, 20);
	push(&root, 30);
	printf("%d popped from stack\n", pop(&root));
	printf("Top element is %d\n", peek(root));

	return 0;
}

OUTPUT:

10 pushed to stack
20 pushed to stack
30 pushed to stack
30 popped from stack
Top element is 20
Elements present in stack : 20 10
...........................................................
Process executed in 3.22 seconds
Press any key to continue.

Advantages of Implementation of Stack using Linked List:

According to the requirements at runtime, the linked list implementation of a stack can expand and contract.
Many virtual machines, including JVM, use it.

Disadvantage of Implementation of Stack using Linked List:

Requires more memory since pointers are used.
In a stack, random accessing is not feasible.

Implementation of Stack using Singly Linked List

All single linked list activities should be carried out according to stack operations LIFO (last in first out), and with the aid of that understanding, we are going to create a stack using a singly linked list.

push()

Get a node started
Update the node's value by adding data, as in node->data = data.
Now update the top pointer to the current node and connect this node to the top of the linked list.

pop()

Check first to see whether there are any nodes in the connected list; if not, return
If not, create a temporary reference to the top node and advance it by one step before releasing the temporary node.

peek()

Verify whether any nodes are present, and if not, return.
Return the value of the linked list's top node if not.

display()

Initialize a temporary node with the top pointer.
now begin navigating temp till NULL is encountered.
Print the value of the temporary node simultaneously.

Example:

#include <stdio.h>
#include <stdlib.h>
struct node {
    int data;
    struct node *next;
}*top;
 
/*
Initialize an empty stack
*/
void initialize() {
    top = NULL;
} 
 
/*
Checks if Stack is empty or not
*/
int isEmpty() {
    if (top == NULL) 
        return 1;
    else
        return 0;
}
 
/*
Returns the top element of Stack
*/
int peek() {
    return top->data;
}
 
/* Count stack elements */
int getStackSize(struct node *head){
    /* Input Validation */
    if (head == NULL) { 
       printf("Error : Invalid stack pointer !!!\n");       
       return;  
    }
      
    int length = 0;
    while(head != NULL){
        head = head->next;
        length++;
    }
    return length;
}
 
/* 
Push an Element in Stack 
*/
void push(int num) {
    struct node *temp;
    temp =(struct node *)malloc(1*sizeof(struct node));
    temp->data = num;
     
    if (top == NULL) {
        top = temp;
        top->next = NULL;
    } else {
        temp->next = top;
        top = temp;
    }
}
 
/*
Pop Operation: Removes Top Element of the Stack
*/
void pop() {
    struct node *temp;
    if (isEmpty(top)) {
        printf("\nStack is Empty\n");
        return;
    } else {
        temp = top;
        top = top->next;
        printf("Removed  Element : %d\n", temp->data);   
        free(temp); 
    }
}
 
/*
 Prints the linked list representation of a stack  
*/
void printStack(struct node *nodePtr) {
  while (nodePtr != NULL) {
     printf("%d", nodePtr->data);
     nodePtr = nodePtr->next;
     if(nodePtr != NULL)
         printf("-->");
  }
  printf("\n");
}
 
void main() {
   /* Initialize Stack */
   initialize();
   /* Push Elements in stack */
   push(1);
   push(2);
   push(3);
   push(4);
   /* Prints Size of Stack */
   printf("Stack Size : %d\n", getStackSize(top));
   /* Printing top element of Stack */
   printf("\nTop Element : %d\n", peek());
   /* Printing Stack */
   printf("Stack as linked List\n");
   printStack(top);
   /* Removing elements from stack */
   pop();
   pop();
   pop();
   pop();
   pop();
   printStack(top);
    
   return;
}

OUTPUT:

Stack Size : 4
Top Element : 4
Stack as linked List
4-->3-->2-->1
Removed  Element : 4
Removed  Element : 3
Removed  Element : 2
Removed  Element : 1
Stack is Empty
....................
Process executed in 4.43 seconds
Press any key to continue

Next TopicSelf-Balancing Binary Search Trees

← prev next →