Level order Traversal in a Binary Tree

A tree is one of the most fundamental data structures. They are used to store and organize data.

A sort of tree data structure known as a binary tree is composed of left and right nodes, each of which can have up to two offspring. Everything starts at the root node, which is the very first node in the tree. A binary tree is a type of tree data structure made up of left and right nodes, each of which has a maximum of two offspring. The root node-the first node in the tree-is where it all begins.

Each node of the tree has the following information:

Information pointing to the left child.

Pointer to the appropriate kid

In the case of a leaf node, the left and right child pointers point to null.

Example:

Algorithm for In-Order traversal :

Traverse the left sub-tree of R In-order.
Process the root R
Traverse the right sub-tree of R In-order.

Let us take an example of a binary tree as given below: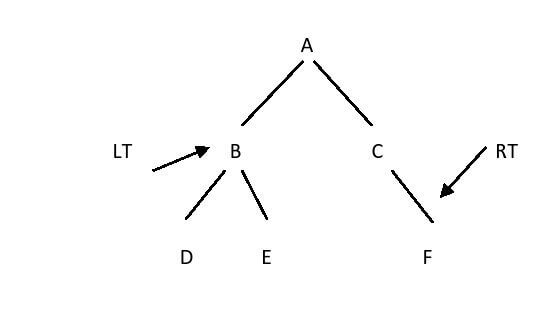

Where LT is Left subtree and RT is Right subtree and A is the root node of binary tree.

DEBACF is an in-order binary tree traversal algorithm.

routine activities-

The following are some typical operations that can be performed on a binary tree:

The common operations that can be carried out on a binary tree are listed in the table below.

1. Insertion:

Any order can be used to add elements to a binary tree. During the initial insertion process, the root node is constructed. The insertions that follow one another recursively search every level of the tree for an empty spot. When it is discovered that a left or right child is empty, the new element is added. As a matter of habit, the insertion always begins from the left child node.

A binary tree can have any order in which elements are added. The root node is created at the initial insertion operation. The insertions that come after each other look for an empty space at every level of the tree recursively.

The new element is added when a left or right child is discovered empty. The insertion always starts from the left child node as a habit.

2. Elimination/Deletion:

Additionally, the binary tree may lose one of its components. Since the elements are not arranged in any particular order, the rightmost element takes its place when a certain node is deleted.

Level order traversal is a technique for traversing binary trees breadth first. We first travel through a node. Because every neighbor node in the current depth must be traversed before moving on to the nodes in the level below, this procedure is known as level order traversal.

Imagine we were given a tree. We will begin by publishing the value of the root node, followed by the value of the root node's children, and so on, printing the values of all the nodes from each level as we move through the tree of level order. Printing every node at the current level of the tree, starting at the top and working our way down, is our main duty. We will process the tree using the first in first out (queue) approach to put this idea into practice. A node's children are then processed and placed in the queue. One by one, each node will be removed, printed, and then its offspring will be put to the queue. A tree is one of the most fundamental data structures. They have a particular task to store and organize the data.

The binary tree can also lose one of its elements. Since the elements are not arranged in any particular order, when a certain node is deleted, the rightmost element takes its place.

Level order traversal is a technique for traversing binary trees breadth first. We first travel through a node. The process is known as level order traversal because it involves going through every neighbor node in the current depth before moving on to the nodes in the following level of the tree.

Let's say that we were given a tree We will begin by publishing the value of the root node, followed by the value of the root node's children, and so on, printing the values of all the nodes from each level as we move through the tree of level order.

Therefore, our primary responsibility is to print the nodes in the current level of the tree, from the first level to the last level. We will use the first in first out (queue) technique to process the tree to accomplish this idea.

A node will be processed, and its children will be added to the queue. We'll remove each node individually, print them, and then add their offspring to the queue. Here is the level order traversal algorithm, which illustrates the full procedure.

C Program:

void level_order_traversal(TreeNode* root)
{
if(root==NULL)
{
return;
}
queue<TreeNode*> q;
q.push(root);
q.push(end);
while(!q.empty())
{
TreeNode* front = q.front();
q.pop();
if(front==end)
{
cout << endl;
if(!q.empty())
q.push(End);
else
break;
}
cout << front->val << " ";
for(auto child: front->childNode)
{
q.push(child);
}
}
}

The following are contained in each node of the tree:

Data
pointer to the left child
Pointer to the right child

The left and right child pointers in the case of a leaf node point to null.

Each form of tree that allows the children at any branch to be organized in a specific order can have an in-order traverse provided for it. In reality, there may be strong reasons to depict the "+" operator as having an arbitrary number of children if you are imagining an expression tree with the nodes being either "+" or "-" operators and the leaves being numerical values or variables. If we permit a single unary child for a specific level of the tree, however, caution must be exercised.

As in most applications of such a tree (such as an expression tree that supports a negation operator or a "-" sign operator), I will regard unary children as a pre-order traversal in the example below. Take into account the tree definition below (defined using go as the template language, but really, any language would be fine here)

type Tree struct{ 
  node TreeNode 
  children []Tree 
} 

Assume that the type TreeNode has a Visit() function.

Continuing to use Go as the template language, we can now define pre-order, in-order, and post-order traversals for this Tree structure:

func (t *Tree) PreOrderTraversal() { 
   t.node.Visit() 
   for _, child := range t.children { 
      child.PreOrderTraversal() 
   } 
} 
 
func (t *Tree) InOrderTraversal() { 
  if len(t.children) == 0 { 
    t.node.Visit() 
    return 
  } 
  if len(t.children) == 1 { 
    t.node.Visit() 
    t.children[0].InOrderTraversal() 
    return 
  } 
  t.children[0].InOrderTraversal() 
  for _, child := range t.children[1:] { 
    t.node.Visit() 
    child.InOrderTraversal() 
  } 
} 
 
func (t *Tree) PostOrderTraversal() { 
  for _, child := range t.children { 
    child.PostOrderTraversal() 
  } 
  t.node.Vist() 
} 

The pre-order and post-order, as you can see, are quite straightforward: you do Visit() before each in pre-order and Visit() after each in post-order. However, in InOrderTraversal(), you visit *between* each element and may really visit the same node more than once. In this situation, care must be exercised, and you must arbitrarily choose whether to visit the node or the kid first. Although I visited the node first in the previous example, your application may warrant making other decisions that are more appropriate.

C++:

/* A binary tree Node

struct Node
{
    int data;
    struct Node* left;
    struct Node* right;
    
    Node(int x){
        data = x;
        left = right = NULL;
    }
};
 */


class Solution
{
    public:
    //Function to return the level order traversal of a tree.
    vector<int> levelOrder(Node* node)
    {
      vector<int> level;
      if(node==NULL)
      return level ;
      queue<Node*> q ;
      q.push(node) ;
      while(!q.empty())
      {
          int size = q.size() ;
          for(int i = 0 ; i<size ; i++)
          {
              Node *a = q.front() ;
              q.pop();
              if(a->left!=NULL)
              q.push(a->left) ;
              if(a->right!=NULL)
              q.push(a->right) ;
              level.push_back(a->data) ;
          }
      }
      return level ;
    }
};

Input:
    1
  /   \ 
 3     2
Output:
1 3 2

Java:

/*
class Node
{
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right = null;
    }
}
*/
class Solution
{
    //Function to return the level order traversal of a tree.
    static ArrayList <Integer> levelOrder(Node root) 
    {
        // Your code here
        ArrayList<Integer> ans = new ArrayList<>();
        Queue<Node> q = new LinkedList<Node>();
        
        if(root == null){
            return ans;
        }
        
        q.offer(root);
        while(!q.isEmpty()){
            // To retrieve and pop the element from queue.
            Node temp = q.poll();
            
            ans.add(temp.data);
            if(temp.left != null){
                q.offer(temp.left);
            }
            if(temp.right != null){
                q.offer(temp.right);
            }
        }
        
        return ans;
    }
}

Output:

Input:
    1
  /   \ 
 3     2
Output:
1 3 2

Python:

class Solution:
    #Function to return the level order traversal of a tree.
    def levelOrder(self,r):
        q=[]
        l=[]
        q.append(r)
        while len(q)!=0:
            r=q.pop(0)
            l+=[r.data]
            if r.left:
                q.append(r.left)
            if r.right:
                q.append(r.right)
        return l

Output:

    Input:
    1
  /   \ 
 3     2
Output:
1 3 2

Overview:

1. What is a tree's level order traversal?

The Level Order Traversal algorithm goes over each node in a tree in order of depth, starting with the root, moving on to its children, etc.

2. How is level order traversal performed?

A queue and node-by-depth traverse can be used to perform level order traversal.

3. Is BFS and Level order traversal equivalent?

Yes, as both algorithms traverse the nodes in depth, they are the same.

4. When is level order traversal appropriate?

As a Breadth-First Search, level order traversal can be used to tackle a variety of graph theory issues, including locating every node inside a single connected component.

Next TopicLowest Common Ancestor of a Binary Tree

← prev next →