Find precedence characters form a given sorted dictionary

Problem statement:

You are given the array of strings which is sorted according to dictionary order. Your task is to determine the order of characters used in this array.

For example:

In the above example, order of the character would be b,d, a,c

So, we have to print the lexicographical ordering of the characters in the form of a string.

Method

To solve the problem, we will compare two words at a time, and the mismatching character will determine the order of characters.

For example, we will compare baa and abcd.

Index 0 of both the strings are different, so we can say that b would come before and after these characters order of remaining characters we can't determine.

We will create a directed graph of characters, and then we will print the topologically sorted order to get our answer.

For example:

In the above example, we will compare two adjacent strings at a time and will try to create a graph.

For i=0 and i=1

We have "baa" and "abcd," and the mismatching character is b,a. So it is for sure b will come before a, and there will be an edge from b to a.

For i=1 and i=2

We have "abcd" and "abca," and the first mismatching character would be 'd' and 'a', so there will be an edge from d to a.

Now graph will look like this:

For i=2 and i=3, we have strings like "abca" and "cba," so the first character which does not match is 'a' and 'c' , so they will draw the edge from node a to node c.

The graph will be: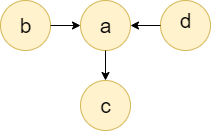

For i=3 and i=4, we have "cab" and "cad" so the mismatched characters are 'b' and 'd'. Now there will be an edge from 'b' to 'd', and both have the edge to the 'a'. So we will modify the graph like this: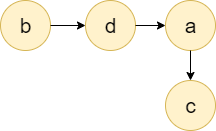

Now, after having the complete iteration, we will get the topologically sorted order of this graph, and that would be "bdac" and that will be our answer.

Java code:

Output:

Explanation

In the above code, we have one function, which returns the answer as a string, and we are printing the result. We use a hashmap of character vs. HashSet in which, for each unique character, we will store its neighbors into a HashSet.

We used another hashmap of character vs. integer to store the indegree (number of incoming edges) to a particular character.

Initially, we stored the indegree of all characters as 0.

Now we are iterating the string array from index 0 to index n-2 and comparing two adjacent strings.

For strings, we will iterate character-wise, and if the characters of both the strings at the same index are not matching, then we will stop.

Now we check if the graph contains the character of string1 or not. If the graph does not contain a character1, then we will add it to the graph, and also, we will put character two as its neighbors into the HashSet of character1.

Also, we will increment the in-degree of character2 by 1.

After creating the graph and indegree of characters, we will get the topological sort of the graph.

We will use Kahn's algorithm to get the topologically sorted order in the breadth-first search order. We will use the queue and put all the characters whose indegree is zero. Now we will iterate into the queue until it is non-empty.

At each time, we will remove the top element of the queue and add it to our answer. We will go to its neighbors and decrement their in-degree by 1. If any neighbors have an in-degree equal to zero, we will add it to our queue.

Thus we will get the topological sort order.

Time complexity: O(N*L), where N is the length of the array and L is the maximum length of the string.

Space complexity: O(N*L)