Printing All Elements in Sorted Order from Row and Column Wise Sorted Matrix.

Matrices are fundamental data structures used to represent two-dimensional arrays. When dealing with matrices that are sorted both row-wise and column-wise, we can efficiently print all elements in sorted order using various approaches. In this article, we'll explore different strategies to achieve this goal using the Java programming language.

Approach 1: Flattening and Sorting

The simplest approach is to flatten the matrix into a one-dimensional array and then sort that array. Here's how to do it:

Flatten the Matrix: Traverse the matrix row by row and add all elements to a one-dimensional array.

Sort the Array: After flattening the matrix, apply a sorting algorithm (e.g., quicksort or mergesort) to sort the array.

Print the Sorted Array: Iterate through the sorted array and print the elements.

This approach is straightforward, but it might not be the most efficient, especially for larger matrices.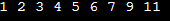

import java.util.*; // importing necessary modules
public class SortedMatrixPrinting {

    public static void main(String[] args) {
        // Define a 2D matrix
        int[][] matrix = {
            {1, 3, 5},
            {2, 6, 9},
            {4, 7, 11}
        };

        // Get the number of rows and columns in the matrix
        int rows = matrix.length;
        int columns = matrix[0].length;

        // Flatten the matrix into a one-dimensional array
        int[] flattenedArray = new int[rows * columns];
        int index = 0;

        // Loop through the rows and columns of the matrix
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                // Store each matrix element in the flattened array
                flattenedArray[index++] = matrix[i][j];
            }
        }

        // Sort the flattened array in ascending order
        Arrays.sort(flattenedArray);

        // Print the sorted elements
        for (int value : flattenedArray) {
            System.out.print(value + " ");
        }
    }
}

Output:

Printing All Elements in Sorted Order from Row and Column Wise Sorted Matrix

In this code:

We define a two-dimensional array matrix that represents the row and column wise sorted matrix.
We calculate the number of rows and columns in the matrix.
We create a one-dimensional array flattenedArray to store the elements of the matrix.
We use nested loops to traverse the matrix and flatten its elements into flattenedArray.
After flattening, we sort the flattenedArray using the Arrays.sort() method.
Finally, we iterate through the sorted array and print its elements.

Time Complexity : O(n*m) + O((n+m)log(n+m))

n*m for traversing the 2D matrix

((n+m)log(n+m)) for sorting the array of size n+m

Space complexity : O(n+m)

Since we are using an additional space to store 2D matrix to 1D matrix

Approach 2: Merge Sorted Arrays

Since the matrix is sorted both row-wise and column-wise, we can treat each row as a sorted array and merge them to get a single sorted array.

Create an Empty Min-Heap: Initialize a min-heap (priority queue) and insert the first element from each row along with the row and column indices.

Extract Minimum and Insert Next: Repeatedly extract the minimum element from the heap, print it, and then insert the next element from the same row (if available). Continue this process until the heap is empty.

import 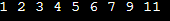java.util.*;

public class SortedMatrixPrinting {

    public static void printSortedMatrix(int[][] matrix) {
        // Get the number of rows and columns in the matrix
        int rows = matrix.length;
        int columns = matrix[0].length;

        // Create a min-heap using a PriorityQueue, with a custom comparator
        // that compares nodes based on their corresponding matrix values
        PriorityQueue<Node> minHeap = new PriorityQueue<>(Comparator.comparingInt(node -> matrix[node.row][node.column]));

        // Initialize the min-heap with the first element from each row
        for (int i = 0; i < rows; i++) {
            minHeap.offer(new Node(i, 0)); // Each node represents the first column of a row
        }

        // Process the heap until it's empty
        while (!minHeap.isEmpty()) {
            // Retrieve the node with the smallest value from the heap
            Node node = minHeap.poll();

            // Print the value of the current node (smallest value)
            System.out.print(matrix[node.row][node.column] + " ");

            // If there are more columns in the current row, add the next element from that row to the heap
            if (node.column + 1 < columns) {
                minHeap.offer(new Node(node.row, node.column + 1)); // Move to the next column of the same row
            }
        }
    }

    // Node class to represent the indices of the matrix
    static class Node {
        int row, column;

        Node(int row, int column) {
            this.row = row;
            this.column = column;
        }
    }

    public static void main(String[] args) {
        // Example input matrix
        int[][] matrix = {
            {1, 3, 5},
            {2, 6, 9},
            {4, 7, 11}
        };

        // Call the printSortedMatrix function to print the matrix elements in sorted order
        printSortedMatrix(matrix);
    }
}

Output:

In this code:

The matrix is traversed row-wise, and the first element from each row is added to the min-heap.
The min-heap automatically organizes the nodes based on their corresponding matrix values due to the custom comparator.
The loop continues until the min-heap is empty, indicating that all elements have been printed.
In each iteration of the loop, the smallest element from the min-heap (the root of the heap) is polled and printed.
If there are more columns left in the row containing the current node, the next element from that row is added to the heap for consideration.

This process continues until all elements have been printed, resulting in the matrix elements being printed in ascending order.

Time Complexity: The time complexity of the "Merge Sorted Arrays" approach is primarily determined by the number of elements in the matrix (m) and the number of rows in the matrix (k):

Merging Step: O(m)

Priority Queue Operations: O(m * log k)

Therefore, the overall time complexity is O(m * log k), where m is the total number of elements in the matrix, and k is the number of rows.

Space Complexity: The space complexity is influenced by the space used to store the priority queue and other variables:

Priority Queue: O(k)

Other Variables: Constant space

Thus, the overall space complexity is O(k), where k is the number of rows.

Next TopicArraylist vs linked list

← prev next →