Applications of Tree in Data Structure

Introduction:

Trees are a fundamental data structure that plays a crucial role in computer science and programming. They provide an efficient way to store and organize data, enabling various applications in different domains.

Overview of Trees

Before diving into the applications, let's briefly review the concept of trees. A tree is a hierarchical data structure consisting of nodes connected by edges. It starts with a root node and branches into child nodes, forming a tree-like structure. Each node can have zero or more child nodes, and the connections between nodes are typically represented as directed edges.

Trees can be classified into various types, such as binary trees, binary search trees, AVL trees, B-trees, and many more. Each type has its specific properties and applications, but they all share the fundamental characteristics of a tree structure.

Applications:

Trees find applications in various domains, including file systems, databases, network routing, and more. Different applications of tree in terms of Binary Search tree, Expression tree, Decision tree, Trie tree, and AVL tree are listed below.

Binary Search Trees

Binary search trees (BSTs) are an important tree data structure widely used in various applications. BSTs have an ordered property where the value of each node is greater than all values in its left subtree and less than all values in its right subtree.

Applications:

The ordering property makes BSTs efficient for searching, insertion, and deletion operations.

They are frequently used in database systems, as well as in implementing dynamic sets and dictionaries.

Binary search trees enable fast searching by traversing the tree based on comparisons with the target value, allowing for logarithmic time complexity.

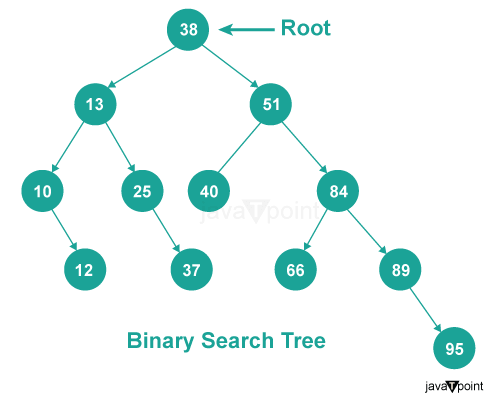
To illustrate the application of trees, let's look at an example of implementing a binary search tree in C++.

#include <iostream>
using namespace std;

// Binary Search Tree Node Definition
struct BSTNode {
    int data;
    BSTNode* left;
    BSTNode* right;
};

// Function to create a new BST node
BSTNode* createNode(int data) {
    BSTNode* newNode = new BSTNode;
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to insert a value into a BST
BSTNode* insertNode(BSTNode* root, int data) {
    if (root == nullptr) {
        return createNode(data);
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }

    return root;
}

// Function to perform in-order traversal of the BST (display elements in ascending order)
void displayInOrder(BSTNode* root) {
    if (root == nullptr) {
        return;
    }

    displayInOrder(root->left);
    cout << root->data << " ";
    displayInOrder(root->right);
}

// Sample usage
int main() {
    BSTNode* root = nullptr;

    root = insertNode(root, 50);
    root = insertNode(root, 30);
    root = insertNode(root, 20);
    root = insertNode(root, 40);
    root = insertNode(root, 70);
    root = insertNode(root, 60);
    root = insertNode(root, 80);

    cout << "Elements in the BST (in-order traversal): ";
    displayInOrder(root);
    cout << endl;

    return 0;
}

Explanation:

The program starts by defining a struct called BSTNode, which represents a node in the binary search tree. Each node contains integer data to store the value and pointers left and right to its left and right children.
The createNode function is used to create a new BST node and initialize its value and children. It takes integer data as input and returns a pointer to the newly created node.
The insertNode function inserts a new node with the given value into the binary search tree. It recursively traverses the tree to find the appropriate position for insertion.
If the value is smaller than the current node's value, it moves to the left child; if the value is greater, it moves to the right child. Once the appropriate position is found, a new node is created and assigned as the child of the current node.
The displayInOrder function performs an in-order traversal of the binary search tree. It recursively visits the left subtree, prints the value of the current node, and then recursively visits the right subtree. This results in the elements being displayed in ascending order.
In the main function, a binary search tree is created by inserting nodes with values 50, 30, 20, 40, 70, 60, and 80.

Program Output:

Expression Trees

Expression trees are used to represent mathematical expressions in a tree-like structure. Each node in the tree represents an operator or an operand, with the leaves being the operands.

Applications:

Expression trees are beneficial for evaluating and manipulating mathematical expressions efficiently.

They find applications in compilers, calculators, and symbolic mathematics.

Expression trees are used in symbolic computation systems, where mathematical expressions are manipulated symbolically rather than being evaluated numerically.

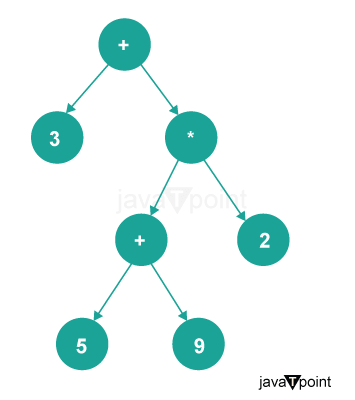
To illustrate the application of trees, let's look at an example of implementing an Expression tree in C++.

#include <iostream>
using namespace std;


// Expression Tree Node Definition
struct ExpTreeNode {
    string value;
    ExpTreeNode* left;
    ExpTreeNode* right;
};

// Function to create a new expression tree node
ExpTreeNode* createNode(string value) {
    ExpTreeNode* newNode = new ExpTreeNode;
    newNode->value = value;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to perform a preorder traversal and print the expression tree
void printExpressionTree(ExpTreeNode* node) {
    if (node == nullptr)
        return;

    cout << node->value << " ";
    printExpressionTree(node->left);
    printExpressionTree(node->right);
}

int main() {
    ExpTreeNode* root = createNode("+");
    ExpTreeNode* child1 = createNode("3");
    ExpTreeNode* child2 = createNode("*");
    ExpTreeNode* grandchild1 = createNode("5");
    ExpTreeNode* grandchild2 = createNode("2");

    root->left = child1;
    root->right = child2;
    child2->left = grandchild1;
    child2->right = grandchild2;

    cout << "Expression Tree: ";
    printExpressionTree(root);
    cout << endl;

    return 0;
}

Explanation:

The program starts by defining a struct called ExpTreeNode, which represents a node in the expression tree.
Each node contains a string value to store the operator or operand and two pointers left and right to point to its left and right children.
The createNode function is used to create a new node and initialize its value and children. It takes a string parameter value and returns a pointer to the newly created node.
The printExpressionTree function performs a preorder traversal of the expression tree and prints the value of each node.
Preorder traversal visits the root node first, followed by the left subtree, and then the right subtree. In this function, the value of the current node is printed, followed by a recursive call to print the left subtree and then the right subtree.
In the main function, an expression tree is constructed by creating nodes and linking them together using pointers.
The root node is created with the value of "+", and additional nodes are created for the operands and operators. The nodes are then connected by assigning the appropriate pointers.
Finally, the printExpressionTree function is called with the root node to print the expression tree in the preorder traversal.

Program Output:

Decision Trees

Decision trees are another popular application of trees in data structures, particularly in machine learning and artificial intelligence.

In a decision tree, each internal node represents a decision based on a specific feature, and each leaf node represents a class label or a numerical value. By traversing the decision tree from the root node to a leaf node, we can make predictions or decisions based on the values of the features.

Applications:

Decision trees provide interpretability and are widely used in fields such as predictive modeling, data mining, and pattern recognition.

They are effective in handling both categorical and numerical data, making them versatile tools for solving various real-world problems.

Decision trees are used for classification and regression tasks by recursively partitioning the data based on feature values.

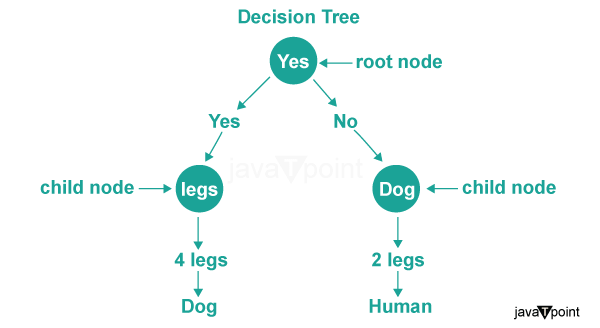
To illustrate the application of trees, let's look at an example of implementing a Decision tree in C++.

#include<iostream> 
using namespace std;

// Decision Tree Node Definition
struct DecisionTreeNode {
    string feature;
    DecisionTreeNode* left;
    DecisionTreeNode* right;
};

// Function to create a new decision tree node
DecisionTreeNode* createNode(string feature) {
    DecisionTreeNode* newNode = new DecisionTreeNode;
    newNode->feature = feature;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to make a decision based on given feature values
string makeDecision(DecisionTreeNode* node, string fur, string legs) {
    if (node == nullptr) {
        return ""; // Invalid decision
    }

    if (node->feature == "fur") {
        if (fur == "yes") {
            return makeDecision(node->left, fur, legs); // Traverse left
        } else if (fur == "no") {
            return makeDecision(node->right, fur, legs); // Traverse right
        }
    } else if (node->feature == "legs") {
        if (legs == "4") {
            return "Dog";
        } else if (legs == "2") {
            return "Human";
        }
    }

    return ""; // Invalid decision
}

// Sample usage
int main() {
    DecisionTreeNode* root = createNode("fur");
    DecisionTreeNode* furYes = createNode("legs");
    DecisionTreeNode* furNo = createNode("legs");

    root->left = furYes;
    root->right = furNo;

    furYes->left = createNode("");
    furYes->right = createNode("");
    furNo->left = createNode("");
    furNo->right = createNode("");

    string fur, legs;
    cout << "Does the animal have fur? (yes/no): ";
    cin >> fur;
    cout << "How many legs does the animal have? (2/4): ";
    cin >> legs;

    string decision = makeDecision(root, fur, legs);
    if (decision == "") {
        cout << "Invalid decision." << endl;
    } else {
        cout << "The animal is a " << decision << "." << endl;
    }

    return 0;
}

Explanation:

The program starts by defining a struct called DecisionTreeNode, which represents a node in the decision tree.
Each node contains a string feature to store the feature to make the decision and two pointers left and right to point to its left and right children.
The createNode function is used to create a new node and initialize its feature and children. It takes a string parameter feature and returns a pointer to the newly created node.
The makeDecision function is used to traverse the decision tree and make a decision based on the given feature values.
It takes a node pointer and two strings representing the values of the "fur" and "legs" features.
The function recursively traverses the tree based on the feature values until it reaches a leaf node, where it returns the classification decision.
In the main function, a decision tree is constructed by creating nodes and linking them together using pointers.
The user is prompted to input the values of the "fur" and "legs" features for an animal. The makeDecision function is called with the root node and the input feature values to determine the classification decision

Program Output:

Trie Trees

Trie trees, also known as prefix trees, are used to store and search for strings efficiently. Each node in the trie represents a character, and the edges represent the next possible characters. By traversing the tree, it is possible to search for words or prefixes of words quickly.

Applications:

They are particularly useful for applications like auto-complete, spell-checking, and dictionary implementations.

Tries trees are utilized in networking and routing protocols for IP address lookup.

Tries trees find applications in text processing tasks such as searching, indexing, and information retrieval.

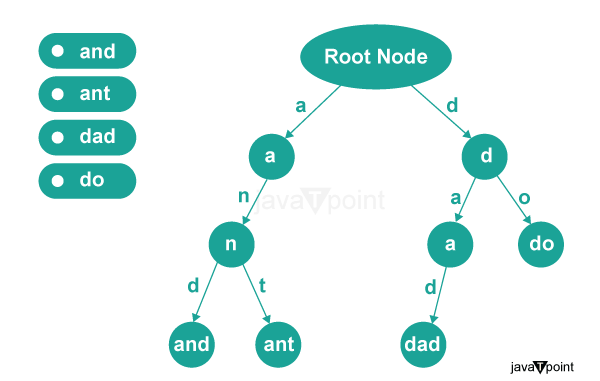
To illustrate the application of trees, let's look at an example of implementing a Trie tree in C++.

#include <iostream>
#include <unordered_map>
#include <vector>

using namespace std;

// Trie Node Definition
struct TrieNode {
    bool isEndOfWord;
    unordered_map<char, TrieNode*> children;
};

// Function to create a new Trie node
TrieNode* createNode() {
    TrieNode* newNode = new TrieNode;
    newNode->isEndOfWord = false;
    return newNode;
}

// Function to insert a word into the Trie
void insertWord(TrieNode* root, string word) {
    TrieNode* curr = root;

    for (char c : word) {
        if (curr->children.find(c) == curr->children.end()) {
            curr->children[c] = createNode();
        }
        curr = curr->children[c];
    }
    curr->isEndOfWord = true;
}

// Function to output all the words in the Trie
void outputWords(TrieNode* root, string prefix = "") {
    if (root == nullptr) {
        return;
    }

    if (root->isEndOfWord) {
        cout << prefix << endl;
    }

    for (const auto& pair : root->children) {
        char c = pair.first;
        TrieNode* child = pair.second;
        outputWords(child, prefix + c);
    }
}

// Sample usage
int main() {
    TrieNode* root = createNode();

    insertWord(root, "apple");
    insertWord(root, "banana");
    insertWord(root, "orange");
    insertWord(root, "pear");

    cout << "Words in the Trie:" << endl;
    outputWords(root);

    return 0;
}

Explanation:

The program starts by defining a struct called TrieNode, which represents a node in the Trie.
Each node contains a boolean flag isEndOfWord to indicate if it represents the end of a word and an unordered map of children to store the child nodes corresponding to different characters.
The createNode function is used to create a new Trie node and initialize its isEndOfWord flag as false.
The insertWord function is used to insert a word into the Trie. It takes a TrieNode pointer root and a string word as input.
The function iterates over each character in the word, checking if the character exists as a child of the current node. If not, a new node is created and added as a child.
The function then moves the current node to the child node corresponding to the current character. Finally, the isEndOfWord flag of the last node representing the end of the word is set to true.
The outputWords function is a recursive function used to output all the words stored in the Trie.
It takes a TrieNode pointer root and a string prefix (optional) as input. The function recursively traverses the Trie, printing the words whenever it encounters a node where isEndOfWord is true.
It also appends the characters of each node to the prefix string to form the complete word.
In the main function, a Trie is created by creating a root node using the createNode Words like "apple", "banana", "orange", and "pear" are inserted into the Trie using the insertWord function.

Program Output:

AVL Trees

AVL trees are self-balancing binary search trees that maintain balance by ensuring that the heights of the left and right subtrees of any node differ by at most one. They ensure that the tree remains balanced, resulting in efficient operations with a time complexity of O(log n).

Applications:

AVL trees find applications in scenarios where maintaining balance is crucial, such as database systems, indexing, and dynamic sets.

By performing rotation and rebalancing operations, AVL trees guarantee optimal performance even with dynamic insertions and deletions.

AVL trees find applications in network routing algorithms, particularly in maintaining routing tables.

To illustrate the application of trees, let's look at an example of implementing an AVL tree in C++.

#include <iostream>
using namespace std;

// AVL Tree Node Definition
struct AVLNode {
    int data;
    int height;
    AVLNode* left;
    AVLNode* right;
};

// Function to create a new AVL node
AVLNode* createNode(int data) {
    AVLNode* newNode = new AVLNode;
    newNode->data = data;
    newNode->height = 1;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to calculate the height of a node
int getHeight(AVLNode* node) {
    if (node == nullptr) {
        return 0;
    }
    return node->height;
}

// Function to calculate the balance factor of a node
int getBalanceFactor(AVLNode* node) {
    if (node == nullptr) {
        return 0;
    }
    return getHeight(node->left) - getHeight(node->right);
}

// Function to perform left rotation
AVLNode* leftRotate(AVLNode* root) {
    AVLNode* newRoot = root->right;
    AVLNode* subtree = newRoot->left;

    newRoot->left = root;
    root->right = subtree;

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;

    return newRoot;
}

// Function to perform right rotation
AVLNode* rightRotate(AVLNode* root) {
    AVLNode* newRoot = root->left;
    AVLNode* subtree = newRoot->right;

    newRoot->right = root;
    root->left = subtree;

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;

    return newRoot;
}

// Function to insert a value into an AVL tree
AVLNode* insertNode(AVLNode* root, int data) {
    if (root == nullptr) {
        return createNode(data);
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    } else {
        return root; // Duplicate values not allowed
    }

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;

    int balance = getBalanceFactor(root);

    // Perform necessary rotations to balance the tree
    if (balance > 1) {
        if (data < root->left->data) {
            return rightRotate(root);
        } else {
            root->left = leftRotate(root->left);
            return rightRotate(root);
        }
    } else if (balance < -1) {
        if (data > root->right->data) {
            return leftRotate(root);
        } else {
            root->right = rightRotate(root->right);
            return leftRotate(root);
        }
    }

    return root;
}

// Function to display the elements of the AVL tree (in-order traversal)
void displayInOrder(AVLNode* root) {
    if (root == nullptr) {
        return;
    }

    displayInOrder(root->left);
    cout << root->data << " ";
    displayInOrder(root->right);
}

// Sample usage
int main() {
    AVLNode* root = nullptr;

    root = insertNode(root, 10);
    root = insertNode(root, 20);
    root = insertNode(root, 30);
    root = insertNode(root, 40);
    root = insertNode(root, 50);
    root = insertNode(root, 25);

    cout << "Elements in the AVL tree (in-order traversal): ";
    displayInOrder(root);
    cout << endl;

    return 0;
}

Explanation:

The program starts by defining a struct called AVLNode, which represents a node in the AVL tree. Each node contains an integer data to store the value, an integer height to store the height of the node, and pointers left and right to its left and right children.
The createNode function is used to create a new AVL node and initialize its values. It takes an integer data as input and returns a pointer to the newly created node.
The getHeight function calculates the height of a node. If the node is nullptr, it returns 0; otherwise, it returns the height value stored in the node.
The getBalanceFactor function calculates the balance factor of a node. It subtracts the height of the right subtree from the height of the left subtree.
The leftRotate function performs a left rotation on the given root node. It reassigns the pointers of the nodes involved in the rotation and updates their heights accordingly.
The rightRotate function performs a right rotation on the given root node. It reassigns the pointers of the nodes involved in the rotation and updates their heights accordingly.
The insertNode function inserts a new node with the given value into the AVL tree. It recursively traverses the tree to find the appropriate position for insertion.
After insertion, it updates the height of the current node and checks for the balance factor. If the balance factor is greater than 1 or less than -1, the necessary rotations are performed to balance the tree.
The displayInOrder function performs an in-order traversal of the AVL tree and prints the elements in ascending order.
In the main function, an AVL tree is created by inserting nodes with values 10, 20, 30, 40, 50, and 25.

Program Output:

Conclusion:

In conclusion, trees are versatile and powerful data structures that find applications in various domains.

Trees provide an effective way to represent hierarchical relationships, such as file systems, organization structures, and XML/HTML parsing.

Binary search trees enable efficient searching of data by organizing elements in a hierarchical order, allowing for quick lookup operations.

Trees, such as AVL trees and red-black trees, facilitate efficient sorting and range query operations on data sets.

Trees can be used as a foundation for implementing various graph algorithms, such as depth-first search (DFS) and breadth-first search (BFS).

Trie trees are useful for efficient string matching, auto-complete functionality, and spell-checking applications.

Decision trees offer a structured approach to decision-making processes, with nodes representing decisions and branches representing possible outcomes.

The applications of trees in data structures are vast and continue to expand as new problem domains and challenges arise. By understanding the characteristics and algorithms associated with trees, developers can leverage their strengths to solve complex problems efficiently and effectively.

Next TopicHow to Check if a Binary Number is Divisible by 3

← prev next →