Priority Queue using Doubly Linked List

Introduction:

A priority queue is a data structure that stores elements with associated priorities and allows for efficient retrieval of the element with the highest (or lowest) priority. While there are various implementations of priority queues, one particularly interesting and flexible approach is to use a doubly linked list to achieve this functionality.

Understanding Priority Queues:

A priority queue is a data structure that stores elements along with their associated priorities. The element with the highest (or lowest) priority can be efficiently retrieved. This makes priority queues suitable for scenarios where elements must be processed based on their priority levels. Examples include task scheduling, job processing, and network routing.

Key operations in a priority queue typically include:

Insertion (Enqueue): Adding an element to the priority queue with a specified priority.
Deletion (Dequeue): Removing the element with the highest priority from the priority queue.
Peek (Front): Viewing the element with the highest priority without removing it.

Priority queues are useful in various applications, such as scheduling processes with different priorities in operating systems, Huffman coding in compression algorithms, Dijkstra's algorithm in graph theory, and more.

There are different variations of priority queues:

Max-Heap: The element with the highest priority has the highest value.
Min-Heap: The element with the highest priority has the lowest value.

The choice between max-heap and min-heap depends on the specific requirements of the application.

Doubly Linked List Overview:

Before diving into the implementation of a priority queue using a doubly linked list, let's briefly review what a doubly linked list is. A doubly linked list is a linear data structure where each element, known as a node, contains a data element and two pointers: one pointing to the next node (next pointer) and another pointing to the previous node (previous pointer). This bidirectional linking allows for easy traversal in both directions.

Implementation of Priority Queue using Doubly Linked List:

Let's implement a basic Priority Queue using a Doubly Linked List in C++. We will define a Node structure for our linked list and a PriorityQueue class to manage the operations.

#include <iostream>
using namespace std;
// Node structure for the doubly linked list
struct Node {
    int data;
    int priority;
    Node* next;
    Node* prev;
    // Constructor to initialize node
    Node(int d, int p) : data(d), priority(p), next(nullptr), prev(nullptr) {}
};
// Priority Queue class using a doubly linked list
class PriorityQueue {
private:
    Node* front;
public:
    // Constructor
    PriorityQueue() : front(nullptr) {}
    // Function to enqueue a new element with priority
    void enqueue(int data, int priority) {
        Node* newNode = new Node(data, priority);
        // If the queue is empty or the new node has higher priority than the front
        if (!front || priority > front->priority) {
            newNode->next = front;
            if (front) front->prev = newNode;
            front = newNode;
        }
        else {
            Node* temp = front;
            // Traverse the list to find the correct position
            while (temp->next && priority <= temp->next->priority) {
                temp = temp->next;
            }
            // Insert the new node
            newNode->next = temp->next;
            if (temp->next) temp->next->prev = newNode;
            temp->next = newNode;
            newNode->prev = temp;
        }
    }
    // Function to dequeue the element with the highest priority
    void dequeue() {
        if (!front) {
            std::cout << "Queue is empty.\n";
            return;
        }
        Node* temp = front;
        front = front->next;
        // Update the previous pointer of the new front
        if (front) front->prev = nullptr;
        // Delete the dequeued node
        delete temp;
    }
    // Function to display the elements of the priority queue
    void display() {
        Node* temp = front;
        while (temp) {
            std::cout << "Data: " << temp->data << ", Priority: " << temp->priority << "\n";
            temp = temp->next;
        }
    }
};
// Driver program
int main() {
    PriorityQueue pq;
    pq.enqueue(10, 2);
    pq.enqueue(20, 1);
    pq.enqueue(30, 3);
    std::cout << "Priority Queue elements:\n";
    pq.display();
    pq.dequeue();
    std::cout << "\nPriority Queue after dequeue:\n";
    pq.display();
    return 0;
}

Explanation:

The program defines a Node structure representing elements in the priority queue, with integer data and priority values.
The PriorityQueue class has a front pointer pointing to the first element in the queue.
The class provides methods to enqueue elements with priorities, dequeue the element with the highest priority, and display the contents of the priority queue.
The enqueue method inserts a new node into the priority queue based on its priority value.
If the queue is empty or the new node has a higher priority than the front element, it becomes the new front. Otherwise, the method traverses the list to find the correct position for the new node.
The dequeue method removes the element with the highest priority (at the front of the queue) and updates the front pointer. The program also includes a display method to print the elements of the priority queue.
In the main function, an instance of the PriorityQueue class is created, and elements with different priorities are enqueued.
The contents of the priority queue are displayed, and then an element is dequeued, followed by another display of the updated priority queue.
The program aims to illustrate the basic operations of a priority queue, where elements are stored based on their priority values.

Program Output: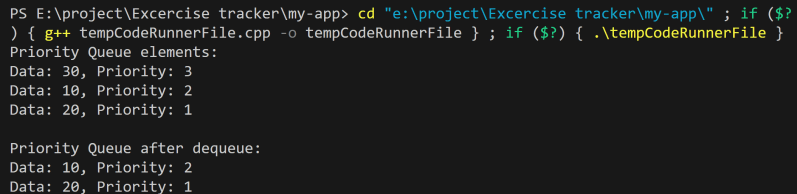

Time Complexity:

Insertion (enqueue):

In the worst case, you may need to traverse the entire linked list to find the correct position to insert the new element.

Time complexity: O(n)

Deletion (dequeue):

Removing the highest priority element requires finding and removing the element with the maximum priority.

If the elements are not sorted, you might need to traverse the entire list to find the maximum priority.

Time complexity: O(n)

Peek (get highest priority element):

If the list is not sorted, you might need to traverse the entire list to find the maximum priority element.

Time complexity: O(n)

Space Complexity:

Storage for elements:

Each element in the priority queue needs space for its data and pointers (for doubly linked list implementation).

Space complexity: O(n)

Additional space:

If you need to store additional information for each element (besides its data), the space complexity may increase accordingly.

Advantages of Using Doubly Linked List:

Efficient Insertion and Deletion:

Inserting an element in a doubly linked list involves adjusting the pointers of the neighboring elements, making it a constant time operation.

Similarly, deleting an element from a doubly linked list is also a constant time operation, given a reference to the node to be deleted.

Flexibility in Traversal:

The bidirectional traversal capability of a doubly linked list allows for efficient searching and manipulation of elements.

Dynamic Memory Management:

Doubly linked lists provide more flexibility in memory management as compared to arrays. Elements can be easily inserted or deleted without the need for contiguous memory.

Ease of Implementation:

Implementing a Priority Queue using a doubly linked list is relatively straightforward, making it an accessible choice for developers.

Conclusion:

In conclusion, implementing a priority queue using a doubly linked list offers several advantages and trade-offs in comparison to other data structures. The use of a doubly linked list allows for efficient insertion and deletion operations at both ends of the list, providing a balanced performance for enqueue and dequeue operations in a priority queue. This flexibility in managing elements makes it suitable for scenarios where dynamic changes to the priority order are frequent.

However, it's essential to acknowledge certain limitations as well. While insertion and deletion operations are efficient, searching for a specific element or determining the priority of a given element may require a linear traversal of the list, resulting in a less optimal time complexity for these operations.

Additionally, the space overhead associated with maintaining two pointers for each element in a doubly linked list should be considered in memory-constrained environments.

Next TopicShortest distance between two cells in a matrix or grid

← prev next →