Intersection Point in Y shaped linked listIntroductionLinked lists are fundamental data structures used in computer science to store and manage collections of data elements. They come in various forms, including singly linked lists, doubly linked lists, and circular linked lists. One interesting variant is the Y-shaped linked list, which presents a unique challenge when it comes to finding the intersection point between two linked lists that share a common segment. Understanding Y-Shaped Linked ListsBefore we dive into intersection points, let's briefly recap what a linked list is. A linked list is a collection of nodes, where each node contains data and a reference (or link) to the next node in the list. A Y-shaped linked list, also called a "Y-junction" linked list, occurs when two linked lists share a common node before diverging into separate paths. Imagine two individual linked lists. At some point, they converge and share nodes for a certain number of elements before branching out again into separate linked lists. This shared node is the intersection point, and it's the heart of our discussion. Formation of Y-Shaped Linked Lists:Y-shaped linked lists can occur due to various reasons. One common scenario is when two separate linked lists merge into a single list. This can happen when two linked lists are concatenated or when multiple linked lists are combined in some way. Consider three separate lists: If we combine List Y and List X to third list, the resulting linked list becomes a Y-shaped linked list. 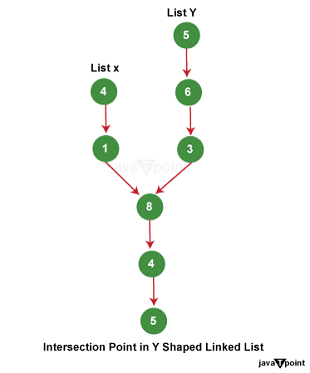
Another scenario is when linked lists represent different paths or branches in a data structure, and they eventually meet at an intersection point. Detecting Intersection PointsDetecting the intersection point in a Y-shaped linked list is a common problem in programming interviews and has several solutions. One straightforward method involves iterating through both linked lists and comparing the nodes one by one. Once the nodes start to differ, the last common node is the intersection point. However, this approach can be inefficient, especially if the linked lists are of varying lengths. A more optimized solution involves finding the lengths of both linked lists and adjusting the starting point of the longer list so that they both have an equal number of nodes to traverse before checking for the intersection. This ensures that when the linked lists are iterated simultaneously, the comparison starts from the point where the lists can intersect. Program:Explanation:
Program output: 
Challenge: Finding the Intersection PointThe challenge arises when we need to determine the intersection point-the node at which the two diverging segments converge and become a single segment. This is particularly complex because, unlike regular linked lists, we can't simply iterate through the lists in a linear manner to find the intersection point. Method 1: HashingOne approach to finding the intersection point in a Y-shaped linked list is by using a hash set. The idea is to traverse one branch of the linked list and store the memory addresses (or references) of the visited nodes in a hash set. Then, traverse the other branch and check if each node's address matches any of the addresses stored in the hash set. The first matching node is the intersection point. While this method is effective, it requires additional memory to store the hash set, and the time complexity can be higher due to multiple iterations. Method 2: Length DifferenceA more efficient method involves finding the difference in lengths of the two branches. First, calculate the lengths of both branches. Then, start traversing from the longer branch by moving ahead by the difference in lengths. After this step, traverse both branches in parallel, checking for the first common node. This node is the intersection point. Method 3: Two PointersAn elegant solution involves using two pointers. Start by placing one pointer at the beginning of each branch. Traverse both branches simultaneously, moving one step at a time for each pointer. When one pointer reaches the end of its branch, move it to the beginning of the other branch. Continue this process until the two pointers meet. The meeting point will be the intersection point. Finding Intersection Points:Detecting the intersection point in a Y-shaped linked list involves traversing the lists while comparing nodes. There are various approaches to accomplishing this:
One way to find the intersection point is by comparing each node of one list with every node of the other list. This involves nested loops and results in a time complexity of O(m * n), where m and n are the lengths of the two lists. While functional, this method is inefficient for larger lists.
Another approach involves using hash tables or sets. While traversing the nodes of the first list, store each node's memory address in a hash set. Then, while traversing the second list, check if the current node's address exists in the hash set. This method reduces the time complexity to O(m + n), making it more efficient than the brute force method.
This technique involves using two pointers, one for each list. Initially, both pointers start at the heads of their respective lists and traverse them. When a pointer reaches the end of its list, it's redirected to the head of the other list. The two pointers will eventually meet at the intersection point. This method has a time complexity of O(m + n) and is efficient in terms of both time and space. Applications of Intersection Points:Understanding intersection points in Y-shaped linked lists has practical applications in various algorithmic challenges: Detecting Cycles in Linked Lists: The technique used to find intersection points can be adapted to detect cycles within a linked list. By considering a linked list as a cycle, you can determine whether a loop exists and locate the starting node of the loop. Finding the Middle Element: The concept of traversing linked lists using two pointers can also be applied to find the middle element of a linked list efficiently. Optimal Meeting Points: In routing algorithms or map navigation, determining optimal meeting points involves finding the intersection of different paths, which can be viewed as a form of intersection point problem. Data Deduplication: In data processing pipelines, linked lists can be used to manage streams of data. Identifying common data points among different streams can help with data deduplication. Conclusion:In conclusion, the concept of intersection points in Y-shaped linked lists is a crucial topic in computer science and data structures. Y-shaped linked lists are a specific configuration of linked lists where two separate chains of nodes converge into a single chain at a certain point, forming a Y shape. Determining the intersection point of such linked lists is a common problem with various real-world applications. Efficiently solving this problem involves understanding and implementing algorithms that utilize pointers and traversal techniques. One widely used approach is the "two-pointer technique," where two pointers traverse the linked lists at different speeds, eventually meeting at the intersection point. This method ensures linear time complexity and minimal space usage. While finding the intersection point in Y-shaped linked lists might seem straightforward, it requires careful consideration of edge cases, such as lists of different lengths or lists with no intersection. As such, algorithm design, analysis, and implementation skills are essential to successfully solve this problem. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









