Design a data structure that supports insert, delete, search, and getRandom in constant timeDesigning a data structure that allows for constant-time insertion, deletion, searching, and random access is an interesting issue in computer science. Obtaining consistent time complexity for these activities sometimes necessitates a trade-off between various characteristics of data storage and access. This article delves into the core principles and potential implementations of several tactics and approaches for building such a data structure. IntroductionData structures are the foundation of effective computing. The pursuit of a data structure with constant temporal complexity for critical operations, including insertion, deletion, search, and random access, has been a focus of algorithmic design. Traditional data structures such as arrays, linked lists, trees, and hash tables each have their advantages, but they often need to give constant time for all of these operations to be performed concurrently. Innovative ways that combine the qualities of these structures are frequently used to accomplish this accomplishment. Requirements Before getting into the design, it's critical to understand the data structure's requirements and constraints:
Possible SolutionsHash Map and Array/List Hash Table In most cases, inserting, deleting, and searching a typical hash table takes O(1) time. However, due to the nature of hash functions, obtaining constant time for random access takes time. A hash table combined with an array or list that allows for random access may fulfill the requirements. Tree with Additional Indexing that is Balanced For most operations, balanced trees such as AVL or Red-Black trees offer O(log n) time complexity. Including an extra indexing mechanism (such as an array of pointers) might allow for constant-time random access. Hash Map Resizable Array A resizable array (such as a list in Python or a vector in C++) can enable constant-time random access. Combining it with a hash map that contains array indices might theoretically offer constant time for all operations. Design: Resizable Array + Hash Map Let's look at a possible solution that combines a resizable array with a hash map to suit the requirements: Data Structure Elements:Resizable Array (ArrayList): An array that modifies its size dynamically to accept items. Hash Map (HashMap): Maps components to their array indices. Operations: Insertion (insert(element)):
Deletion (delete(element)):
Search (search(element)):
GetRandom (getRandom()):
Analysis of Complexity Insertion, deletion, search, and GetRandom: Each of these actions requires constant-time access to the hash map and the array, ensuring that the O(1) complexity condition is met. ImplementationOutput: 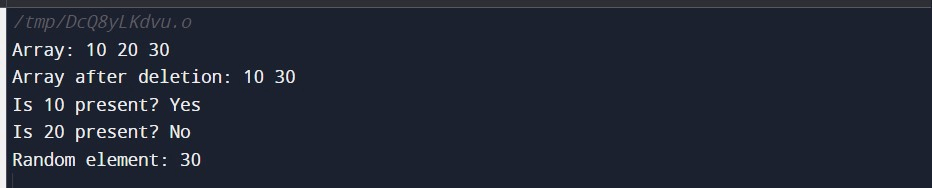
Explanation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









