DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Number of ways to traverse an N-arrEach node in a N-ary tree, a flexible tree data structure, can contain a variable number of child nodes, usually up to N. In comparison, nodes in binary trees can have a maximum of two children. N-ary trees allow for more complicated hierarchical structures because each node can have numerous child nodes, and the root node acts as the starting point for navigating the tree. Depending on the exact traversal order you select, there are a variety of ways to navigate a N-ary tree. Preorder, postorder, and in-order traversal ordering are frequently used for trees. The number of nodes in the tree determines how many methods there are to traverse an N-ary tree in each of these orders. Therefore, there are 'n!' ways to traverse an N-ary tree with 'n' nodes for each of these three typical traversal orders. There are 'n!' various node configurations for every traversal order. Each order corresponds to a different layout. Problem: Determine how many paths there are from the root vertex of an n-ary tree (or a Directed Acyclic Graph) to any other vertex. 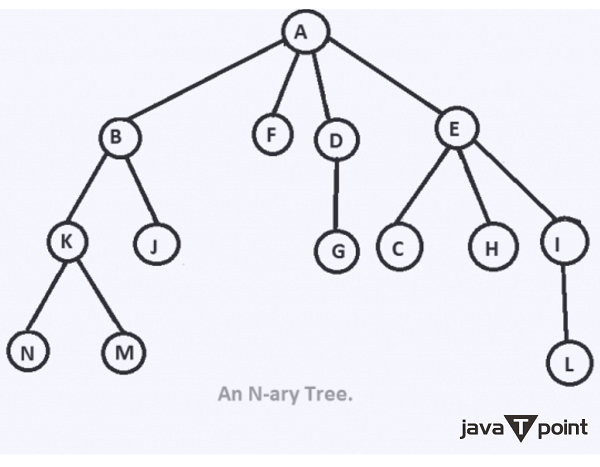
Note: The problem can also be asked on a Directed Acyclic Graph. The approach would remain the same.The task at hand is to determine how many paths there are to traverse the entire tree, beginning at the root vertex. Such methods can be numerous. Following is a list of a few of them. The traversal order is N->M->K->J->B->F->D->E->C->H->I->L->A (sort of depth-first). Level order traversal: A->B->F->D->E->K->J->G->C->H->I->N->M->L. Note: The product of the factorials of the number of offspring of each node yields the total number of traversal paths. Please refer to the following figure for a clear comprehension: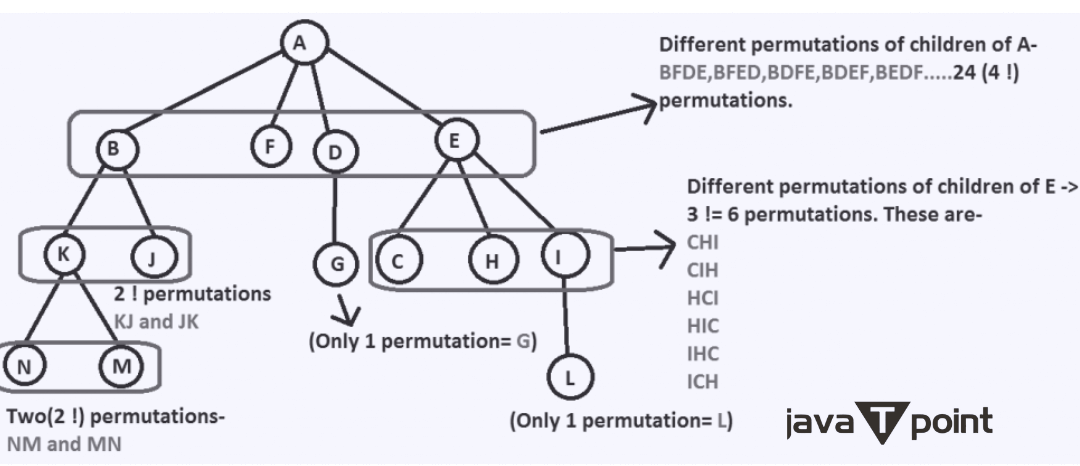
Here, "A" has four kids; hence, there are four different permutations. Since "B" has two kids, there are two possible permutations. There are 0! potential permutations as 'F' is childless. Thus, all of these methods are 4- 4! There are 576 ways to do this: * 2! * 0! * 1! * 3! * 2! * 0! * 0! * 0! * 1! * 0! * 0! There are a tonne of methods, but only a select few-in order, level-order, preorder, and postorder-prove to be helpful. The order is based on how prevalent these traversals are. Follow the below steps to solve the problem:
Implementation:Code in java: Output: Number of ways to traverse the tree: 6912 The Java application uses an algorithm like breadth-first search to calculate the number of ways to traverse an N-ary tree. It specifies a list of children and a key for the node structure. The calculateWays function traverses the tree and records traversal options. It starts with one way and multiplies the ways by the factorial of the number of children at each node to process each node. Next, the computer builds an example N-ary tree and discovers 6912 traversal paths across it. The output illustrates how versatile N-ary tree structures are for a range of applications by revealing the enormous number of distinct traversal sequences that are conceivable within the tree. Time Complexity: O(N2). By calculating the factorials of every number from 1 to N, we can optimize the solution to work in O(N) time. Auxiliary space: O(N) |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









