Lowest Common Ancestor of a Binary Tree

What does the binary tree's lowest common ancestor represent?

The lowest node in the tree that contains both n1 and n2 as descendants is the lowest common ancestor (LCA), and n1 and n2 are the nodes for which we are looking for the LCA. As a result, the common ancestor of nodes n1 and n2 that is placed the furthest from the root is the LCA of a binary tree containing nodes n1 and n2.

LCA (Lowest Common Ancestor) application:

The gap between pairs of nodes in a tree can be computed as the distance from the root to n1 plus the distance from the root to n2 minus twice the distance from the root to their lowest common ancestor.

Example: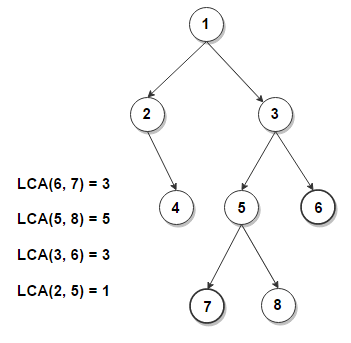

Approach-

We know that because this is a Binary Search Tree, the left node will be less than or equal to the root node and the right node will be higher than the root node. In essence, this entails investigating the edge instances below:
Return null if the root is empty.
The LCA is the root node if one of the nodes is the root node (Lowest Common Ancestor)
The Root is the LCA if one node is greater than the root and another is less than the root.
There is no LCA if the two provided nodes are identical. deliver null.
Call the LCA function iteratively to compute steps 1 through 4 on the left node of the root if both nodes are smaller than the root.
Call the LCA function iteratively to compute steps 1 through 4 on the right node of the root if both nodes are greater than the root.

Program in C++:

Recursive Approach Using single Traversal

Time complexity:

O(n)

Space complexity:

O(n)

Function to print LCA:

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL) return NULL ; 
        //if i get p i will return it 
        if(root==p) return p ;
        //if i get q i will return it 
        if(root==q) return q ;
 
      //make left call 
      TreeNode*leftcall = lowestCommonAncestor(root->left,p,q) ; 
      //make right call 
     TreeNode*rightcall = lowestCommonAncestor(root->right,p,q) ;

         //if at a node both leftcall and rightcall returned NULL--> return NULL
         if(leftcall==NULL and rightcall==NULL)  return NULL ; 


         //if at a node leftcall returns found node and rightcall returned NULL--> return leftcall
         if(leftcall!=NULL and rightcall==NULL)  return leftcall ; 

      //if at a node leftcall returned NULL and rightcall returned found node--> return rightcall
         if(leftcall==NULL and rightcall!=NULL)  return rightcall ; 

      //if at a node both leftcall and rightcall returned found node--> return current node
         if(leftcall!=NULL and rightcall!=NULL)  return root ;

      return root;
    }
};

Input:

Output:

Iterative Approach

Using Double Traversal and finding path for node p and q respectively than comparing their path to find LCA.

Complexity

Time complexity:

O(n)+O(n)

Space complexity:

O(n)+O(n)

Function to print LCA:

class Solution {
public:
//find path of both p and q 
bool findPath(TreeNode*root , vector<int>&path,TreeNode*toSearch){

    if(root==NULL){
        return 0;
    }
   
   //Always store current node when moving from one path to other later we will remove if coming back with false 
    path.push_back(root->val);
   
   //if found
     if(root->val == toSearch->val){
         return true;
     }

    //see if toSearch for is found in any path return true
   bool leftSearch =  findPath(root->left,path,toSearch);
   bool rightSearch =  findPath(root->right,path,toSearch);

   if(leftSearch==true || rightSearch==true){
         return true;
     }

    //return false and remove last added node 
    path.pop_back();
    return false;
}
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL){
            return NULL;
        }
          TreeNode*node = root;
        vector<int>pathforp , pathforq ; 

        bool resultLeft = findPath(root,pathforp,p);
        bool resultRight =findPath(root,pathforq,q);
        
      //  for(auto it : pathforp) cout<<it<<" ";
      //  cout<<"\n";
       // for(auto itr : pathforq) cout<<itr<<" ";
      // cout<<"\n";

        //if any p or q not found 
        if(resultLeft == false || resultRight==false) {
            return NULL;
        }
   
        //else path is present  
        bool check = 0;
        for(int i=0; i<pathforp.size() and i<pathforq.size() ; i++){
              if(pathforp[i]!=pathforq[i]){
                  //i.e just previous value is answer 
                  node->val = pathforp[i-1];
                  check=1;
                    break;
                     }
        }
       if(!check){
           int mini = min(pathforp.size() , pathforq.size()) ;
         node->val = pathforp[mini-1]; //i.e both p and q were equal so return last value of smaller path as check=0
         /* [1,2] , p=2 , q=1
        pathforp ->  1 2 
        pathforq ->  1
        ans = 1
         */
       }  
        return node; //we can also return root
    }
};

Input:

Output:

Function to print LCA in Python:

class Solution:
    def lowestCommonAncestor(self, root, n1, n2):
        if root is None:
            return None

        if root.val == n1.val or root.val == n2.val:
            return root

        leftans = self.lowestCommonAncestor(root.left, n1, n2)
        rightans = self.lowestCommonAncestor(root.right, n1, n2)

        if leftans is not None and rightans is not None:
            return root
        elif leftans is not None:
            return leftans
        elif rightans is not None:
            return rightans
        else:
            return None

Input:

Output:

Function to print LCA in Java:

class Solution {
  public TreeNode lowestCommonAncestor(TreeNode root, TreeNode n1, TreeNode n2) {
    if (root == null || root == n1 || root == n2) {
      return root;
    }

    TreeNode leftans = lowestCommonAncestor(root.left, n1, n2);
    TreeNode rightans = lowestCommonAncestor(root.right, n1, n2);

    if (leftans != null && rightans != null) {
      return root;
    } else if (leftans != null) {
      return leftans;
    } else {
      return rightans;
    }
  }
}

Input:

Output:

Next TopicTop View of a Binary Tree

← prev next →