Elements to be added so that all elements of a range are present in the array
Given an array with N elements, identify the smallest (A) and largest (B) values within the array. The objective is to determine the minimum number of elements that need to be added to the array to ensure that all numbers within the range [A, B] are present at least once.
Note: Before looking into the solution, try to come up with an approach to find multiple approaches to the same problem, which ultimately enhances your coding skills
Method 1 (Sorting):
- Begin by arranging the elements in the array in ascending order.
- Iterate through the sorted array and check if the difference between arr[i] and arr[i+1] is equal to 1. If it's not equal to 1, update a counter (count) by calculating the difference as count = arr[i+1] - arr[i] - 1.
- Finally, return the value of the count variable.
This method involves sorting the array and then counting the gaps between consecutive elements to determine how many numbers need to be added to fill those gaps.
Java Implementation:
Output:

Time Complexity: O(n log n) // for sorting
Auxiliary Space: O(1)
Method 2 :
- Start by creating a hash data structure to keep track of the elements in the array.
- Keep two variables to store the minimum and maximum elements found in the array.
- Iterate through the range of numbers from the minimum to the maximum element.
- For each number in the range, check if it exists in the hash. If it doesn't exist, increment a counter to keep track of the count.
- Finally, return the value of the counter.
This method involves using a hash to efficiently determine the count of missing numbers within the specified range.
Java Implementation:
Output:

Time Complexity:
- The time complexity of this code is O(N) for both operations:
- Building the hash set (HashSet<Integer> set) from the array takes O(N) time because it involves iterating through the array once.
- The second loop iterates from minm to maxm, a constant-sized range based on the input data. Therefore, this loop also takes O(N) time.
- The overall time complexity is O(N).
Space Complexity:
- The space complexity of this code is also O(N) for the following reasons:
- The HashSet<Integer> set is used to store the elements from the array. In the worst case, where all elements are distinct, it can store all N elements. Therefore, the space complexity for the hash set is O(N).
- The additional variables count, maxm, and minm occupy constant space and do not depend on the input size.
- The overall space complexity is O(N).
Method 3 (Using a Boolean Array):
- We can create a Boolean array and initialize all its values to "false."
- Next, we iterate through the input array, and for each number falling within the range [A, B], we set the corresponding element in the Boolean array to "true."
- To find the count of missing numbers in the range [A, B], we count the occurrences of "false" values in the Boolean array. This count represents the number of elements we must add to the input array to ensure that all numbers in the range [A, B] are present at least once.
- This approach relies on marking the presence of numbers within the specified range using a Boolean array and then counting the remaining "false" values to determine the required additions.
Java Implementation:
Output:
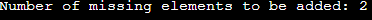
Explanation:
- First, we find the minimum and maximum values in the input array. These values determine the range of numbers we're interested in covering.
- Next, we create a boolean array to represent this range. Each element in this array corresponds to a number within the specified range, and we initialize them as 'false' to indicate that none of them are present yet.
- We then go through the input array, and for each number within the specified range, we mark it as 'present' by changing the corresponding element in our boolean array to 'true'.
- Once we've marked all the numbers in the array within our target range, we count the remaining 'false' elements in the boolean array. This count represents the number of elements we must add to the array to cover all the numbers within the specified range.
- Finally, we return this count as the result.
Time Complexity:
- The code iterates through the input array once to find the minimum and maximum values, which takes O(N) time, where N is the length of the input array.
- It then iterates through the input array again to mark numbers within the specified range and count missing elements. This also takes O(N) time.
- The total time complexity is O(N), where N is the size of the input array.
Space Complexity:
- The space complexity is primarily determined by the boolean array isElementPresent, which has a size equal to the range of numbers from the minimum to the maximum value in the input array (i.e., maxElement - minElement + 1).
- Therefore, the space complexity is O(R), where R is the range of numbers in the input array, which could be significantly smaller than N in most cases.
- Other variables and data structures used in the code have constant space requirements.
|


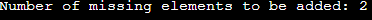
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









