Spanning tree

In this article, we will discuss the spanning tree and the minimum spanning tree. But before moving directly towards the spanning tree, let's first see a brief description of the graph and its types.

Graph

A graph can be defined as a group of vertices and edges to connect these vertices. The types of graphs are given as follows -

• Undirected graph: An undirected graph is a graph in which all the edges do not point to any particular direction, i.e., they are not unidirectional; they are bidirectional. It can also be defined as a graph with a set of V vertices and a set of E edges, each edge connecting two different vertices.
• Connected graph: A connected graph is a graph in which a path always exists from a vertex to any other vertex. A graph is connected if we can reach any vertex from any other vertex by following edges in either direction.
• Directed graph: Directed graphs are also known as digraphs. A graph is a directed graph (or digraph) if all the edges present between any vertices or nodes of the graph are directed or have a defined direction.

Now, let's move towards the topic spanning tree.

What is a spanning tree?

A spanning tree can be defined as the subgraph of an undirected connected graph. It includes all the vertices along with the least possible number of edges. If any vertex is missed, it is not a spanning tree. A spanning tree is a subset of the graph that does not have cycles, and it also cannot be disconnected.

A spanning tree consists of (n-1) edges, where 'n' is the number of vertices (or nodes). Edges of the spanning tree may or may not have weights assigned to them. All the possible spanning trees created from the given graph G would have the same number of vertices, but the number of edges in the spanning tree would be equal to the number of vertices in the given graph minus 1.

A complete undirected graph can have n^n-2 number of spanning trees where n is the number of vertices in the graph. Suppose, if n = 5, the number of maximum possible spanning trees would be 5^5-2 = 125.

Applications of the spanning tree

Basically, a spanning tree is used to find a minimum path to connect all nodes of the graph. Some of the common applications of the spanning tree are listed as follows -

• Cluster Analysis
• Civil network planning
• Computer network routing protocol

Now, let's understand the spanning tree with the help of an example.

Example of Spanning tree

Suppose the graph be -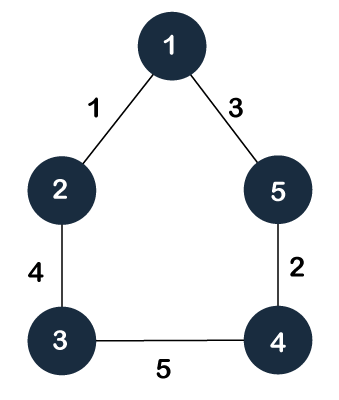

As discussed above, a spanning tree contains the same number of vertices as the graph, the number of vertices in the above graph is 5; therefore, the spanning tree will contain 5 vertices. The edges in the spanning tree will be equal to the number of vertices in the graph minus 1. So, there will be 4 edges in the spanning tree.

Some of the possible spanning trees that will be created from the above graph are given as follows -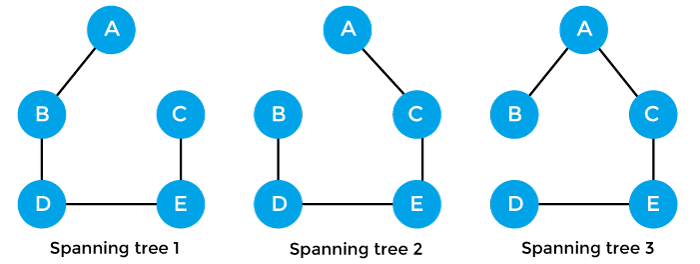

Properties of spanning-tree

Some of the properties of the spanning tree are given as follows -

• There can be more than one spanning tree of a connected graph G.
• A spanning tree does not have any cycles or loop.
• A spanning tree is minimally connected, so removing one edge from the tree will make the graph disconnected.
• A spanning tree is maximally acyclic, so adding one edge to the tree will create a loop.
• There can be a maximum n^n-2 number of spanning trees that can be created from a complete graph.
• A spanning tree has n-1 edges, where 'n' is the number of nodes.
• If the graph is a complete graph, then the spanning tree can be constructed by removing maximum (e-n+1) edges, where 'e' is the number of edges and 'n' is the number of vertices.

So, a spanning tree is a subset of connected graph G, and there is no spanning tree of a disconnected graph.

Minimum Spanning tree

A minimum spanning tree can be defined as the spanning tree in which the sum of the weights of the edge is minimum. The weight of the spanning tree is the sum of the weights given to the edges of the spanning tree. In the real world, this weight can be considered as the distance, traffic load, congestion, or any random value.

Example of minimum spanning tree

Let's understand the minimum spanning tree with the help of an example.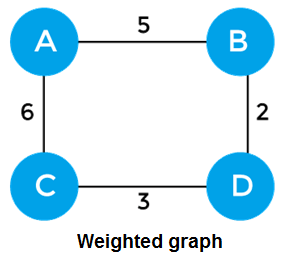

The sum of the edges of the above graph is 16. Now, some of the possible spanning trees created from the above graph are -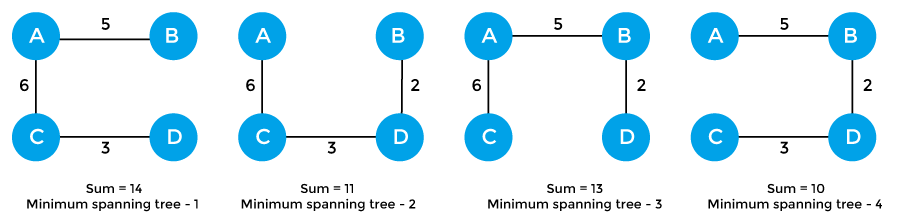

So, the minimum spanning tree that is selected from the above spanning trees for the given weighted graph is -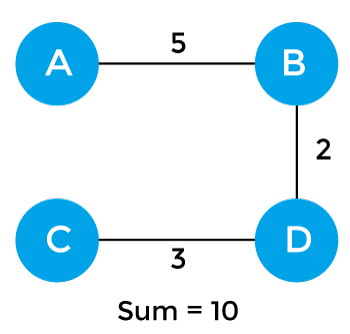

Applications of minimum spanning tree

The applications of the minimum spanning tree are given as follows -

• Minimum spanning tree can be used to design water-supply networks, telecommunication networks, and electrical grids.
• It can be used to find paths in the map.

Algorithms for Minimum spanning tree

A minimum spanning tree can be found from a weighted graph by using the algorithms given below -

• Prim's Algorithm
• Kruskal's Algorithm

Let's see a brief description of both of the algorithms listed above.

Prim's algorithm - It is a greedy algorithm that starts with an empty spanning tree. It is used to find the minimum spanning tree from the graph. This algorithm finds the subset of edges that includes every vertex of the graph such that the sum of the weights of the edges can be minimized.

To learn more about the prim's algorithm, you can click the below link - https://www.javatpoint.com/prim-algorithm

Kruskal's algorithm - This algorithm is also used to find the minimum spanning tree for a connected weighted graph. Kruskal's algorithm also follows greedy approach, which finds an optimum solution at every stage instead of focusing on a global optimum.

To learn more about the prim's algorithm, you can click the below link - https://www.javatpoint.com/kruskal-algorithm

So, that's all about the article. Hope the article will be helpful and informative to you. Here, we have discussed spanning tree and minimum spanning tree along with their properties, examples, and applications.