Prim's AlgorithmIn this article, we will discuss the prim's algorithm. Along with the algorithm, we will also see the complexity, working, example, and implementation of prim's algorithm. Before starting the main topic, we should discuss the basic and important terms such as spanning tree and minimum spanning tree. Spanning tree - A spanning tree is the subgraph of an undirected connected graph. Minimum Spanning tree - Minimum spanning tree can be defined as the spanning tree in which the sum of the weights of the edge is minimum. The weight of the spanning tree is the sum of the weights given to the edges of the spanning tree. Now, let's start the main topic. Prim's Algorithm is a greedy algorithm that is used to find the minimum spanning tree from a graph. Prim's algorithm finds the subset of edges that includes every vertex of the graph such that the sum of the weights of the edges can be minimized. Prim's algorithm starts with the single node and explores all the adjacent nodes with all the connecting edges at every step. The edges with the minimal weights causing no cycles in the graph got selected. How does the prim's algorithm work?Prim's algorithm is a greedy algorithm that starts from one vertex and continue to add the edges with the smallest weight until the goal is reached. The steps to implement the prim's algorithm are given as follows -
The applications of prim's algorithm are -
Example of prim's algorithmNow, let's see the working of prim's algorithm using an example. It will be easier to understand the prim's algorithm using an example. Suppose, a weighted graph is - 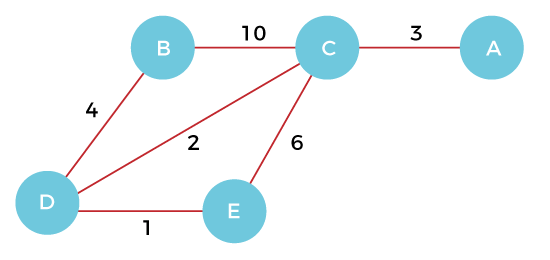
Step 1 - First, we have to choose a vertex from the above graph. Let's choose B. 
Step 2 - Now, we have to choose and add the shortest edge from vertex B. There are two edges from vertex B that are B to C with weight 10 and edge B to D with weight 4. Among the edges, the edge BD has the minimum weight. So, add it to the MST. 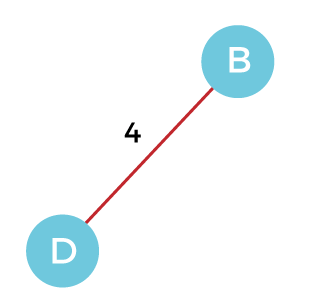
Step 3 - Now, again, choose the edge with the minimum weight among all the other edges. In this case, the edges DE and CD are such edges. Add them to MST and explore the adjacent of C, i.e., E and A. So, select the edge DE and add it to the MST. 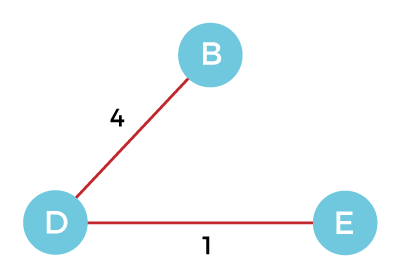
Step 4 - Now, select the edge CD, and add it to the MST. 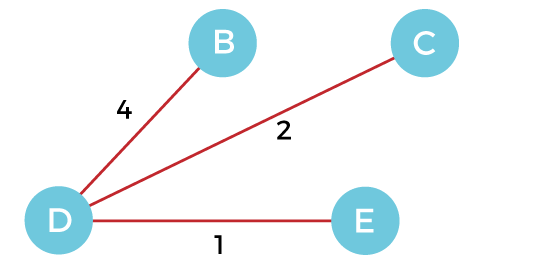
Step 5 - Now, choose the edge CA. Here, we cannot select the edge CE as it would create a cycle to the graph. So, choose the edge CA and add it to the MST. 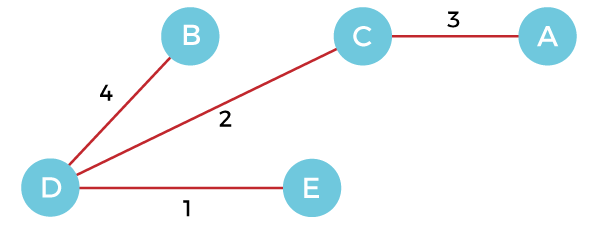
So, the graph produced in step 5 is the minimum spanning tree of the given graph. The cost of the MST is given below - Cost of MST = 4 + 2 + 1 + 3 = 10 units. AlgorithmComplexity of Prim's algorithmNow, let's see the time complexity of Prim's algorithm. The running time of the prim's algorithm depends upon using the data structure for the graph and the ordering of edges. Below table shows some choices -
Prim's algorithm can be simply implemented by using the adjacency matrix or adjacency list graph representation, and to add the edge with the minimum weight requires the linearly searching of an array of weights. It requires O(|V|2) running time. It can be improved further by using the implementation of heap to find the minimum weight edges in the inner loop of the algorithm. The time complexity of the prim's algorithm is O(E logV) or O(V logV), where E is the no. of edges, and V is the no. of vertices. Implementation of Prim's algorithmNow, let's see the implementation of prim's algorithm. Program: Write a program to implement prim's algorithm in C language. Output 
So, that's all about the article. Hope, the article will be helpful and informative to you.
Next TopicKruskal's Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









