K-way Merge Sort

Introduction

K-way merge sort is a sophisticated sorting algorithm that extends the merge sort approach. The goal of the k-way merge problem is to combine k-sorted arrays into one sorted array that has the same elements. While the traditional merge sort algorithm merges two subarrays at a time, the K-way merge sort merges K subarrays, which leads to better performance when dealing with vast amounts of data.

This algorithm is handy when handling large datasets, as it can efficiently sort and merge multiple subarrays, leading to improved efficiency and faster processing times. The K-way merge sort algorithm is a powerful tool in computer science and is widely used in various applications that require sorting large data sets.

Algorithm

The K-way merge sort algorithm can be broken down into the following steps:

Divide: The original array is divided into K subarrays of approximately equal size.
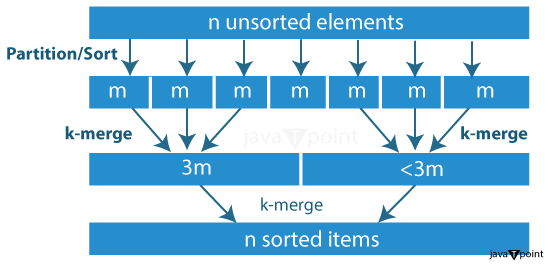
Conquer: Each of these subarrays is sorted individually. This can be done using any sorting algorithm, but for efficiency, we typically use a recursive application of the K-way merge sort.
Combine: The sorted subarrays are merged like the one used in traditional merge sort. However, instead of merging two arrays simultaneously, we merge K arrays using a min-heap data structure

Pseudocode

Here is a simple pseudocode representation of the K-way merge sort algorithm:

function kWayMergeSort(array, k)
    if array.length <= k
        return insertionSort(array)
    else
        subarrays = splitArrayIntoK(array, k)
        for i in 0 to k-1
            subarrays[i] = kWayMergeSort(subarrays[i], k)
        return mergeSubarrays(subarrays, k)

Example in JavaScript:

function kWayMergeSort(arr, k) {
    if (arr.length <= 1) {
        return arr;
    }

    let mid = Math.ceil(arr.length / k);
    let chunks = [];
    for (let i = 0; i < k; i++) {
        chunks.push(arr.slice(i * mid, (i + 1) * mid));
    }

    for (let i = 0; i < k; i++) {
        chunks[i] = kWayMergeSort(chunks[i], k);
    }

    return mergeKSortedArrays(chunks);
}

function mergeKSortedArrays(arrs) {
    let merged = [];
    let pointers = new Array(arrs.length).fill(0);

    while (true) {
        let minVal = Infinity;
        let minIdx = -1;
        for (let i = 0; i < arrs.length; i++) {
            if (pointers[i] < arrs[i].length && arrs[i][pointers[i]] < minVal) {
                minVal = arrs[i][pointers[i]];
                minIdx = i;
            }
        }

        if (minIdx === -1) {
            break;
        }

        merged.push(minVal);
        pointers[minIdx]++;
    }

    return merged;
}

let arr = [10, 2, 5, 3, 7, 13, 1, 6];
let k = 3;
console.log(kWayMergeSort(arr, k)); 

Output:

[1, 2, 3, 5, 6, 7, 10, 13]

This script first divides the input array into K chunks and sorts each chunk recursively using the kWayMergeSort function. Then, it merges all the sorted chunks into one sorted array using the mergeKSortedArrays function. The mergeKSortedArrays function uses a pointer for each chunk to track which elements have been included in the merged array. It repeatedly selects the smallest element from the chunks and adds it to the merged array, updating the corresponding pointer. The process continues until all elements from all chunks have been added to the merged array. It's always recommended to understand the algorithm thoroughly and adjust the implementation according to your specific needs.

Time Complexity

K-way merge sort is more efficient than traditional merge sort. Its time complexity is O(n logk n), where n is the number of elements in the array. This efficiency is particularly noticeable when K is greater than 2 and there is a significant amount of data.

Space Complexity

During the process of the K-way merge sort, multiple subarrays are created, and a min-heap is used to merge the subarrays efficiently. However, to accomplish this task, additional space is required to store the subarrays and the min-heap. As a result, the K-way merge sort has a space complexity of O(n), which can impact the algorithm's performance when dealing with large datasets.

Conclusion

K-way merge sort is an advanced sorting algorithm that breaks the input dataset into K number of smaller sub-lists, each of which is sorted individually. These sub-lists are then merged to obtain the final sorted output. This approach helps to reduce the overall time complexity of the sorting process and makes it particularly useful when dealing with large datasets. By leveraging the power of divide-and-conquer and the efficiency of a min-heap, K-way merge sort provides a significant performance improvement over traditional sorting algorithms, especially when working with large values of K.

Next TopicMaximize Total Score

← prev next →