Diagonal Traversal of Binary TreeHere we will see how we can traverse diagonally in a binary tree. To print the diagonal nodes in a binary tree, we need to calculate the diagonal distance. Let's understand this through an example. Consider the below tree:In the above tree, the diagonal distance is represented by using the notation 'd'. There are two rules for marking the diagonal distance:
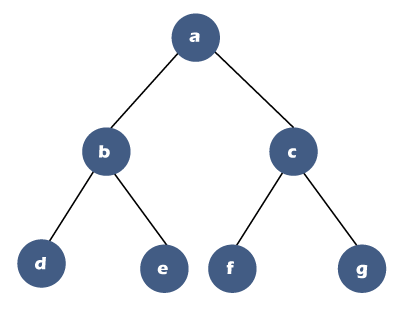
In the above tree, the diagonal distance of node 'a' is 0. Since the node 'a' has two children, i.e., node 'b' (left child) and node 'c' (right child), so the diagonal distance for the node 'b' gets incremented and becomes 1, whereas the diagonal distance for the node 'c' would remain same and becomes 0. The node 'b' has a left child, i.e., d, and its diagonal distance would become 2, while the node 'e' is the right child, so its diagonal distance value would remain the same, i.e., 1. The node 'c' has a left child, i.e., f, so its diagonal distance value gets incremented, and 'd' value of 'f' would become 1. The node 'c' has also the right child, i.e., 'g' and its diagonal distance value would remain the same as its parent, i.e., 'c'. Once the diagonal distance of all the nodes is calculated, we will find out the diagonals. The nodes that are having the same value of diagonal distance will be considered as a diagonal. In the above tree, we can observe that the nodes 'a', 'c', and 'g' have the same diagonal distance value so "acg" would be considered as a diagonal. The nodes 'b', 'e' and 'f' have the same diagonal distance value, i.e., 1, so "aef" would be considered as a diagonal. Only one node with a diagonal distance value is 2. Therefore, there are three diagonals in the above binary tree: "acg", "bef", and "d". Consider the below tree to understand the marking of nodes with the diagonal distance more clearly.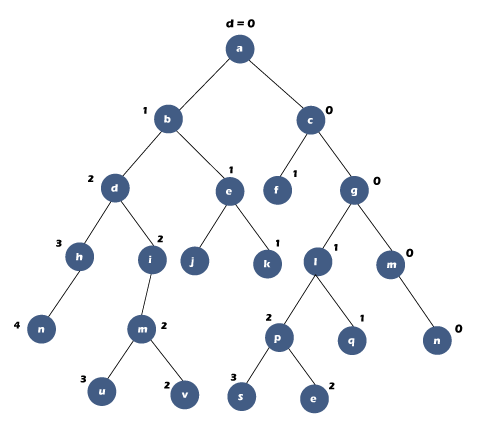
In the above binary tree, the nodes with a diagonal distance value 0 are 'a', 'c', 'g', 'm' and 'r'. The nodes with a diagonal distance value 1 are 'b', 'e', 'f', 'k', 'l' and 'q'. The nodes with a diagonal distance value 2 are 'd', 'i', 'j', 'm', 'p', 'v' and 't'. The nodes with a diagonal distance value 3 are 'h', 'u', and 's'. There is only one node with a value 4 is 'n'. Therefore, there exist 5 diagonals that are "a c g m r", "b e f k l q", "d i j m p v t", "h u s" and "n". Short trick to mark the node with a diagonal distance value:
AlgorithmConsider the below tree to understand the above algorithm more clearly.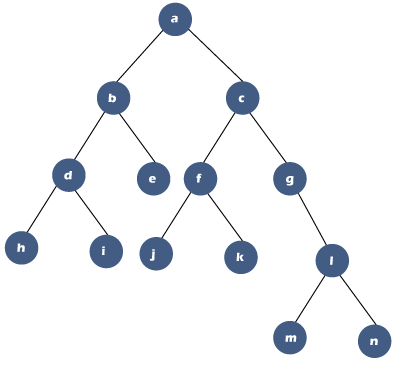
Here we take Queue data structure for printing the diagonal elements. According to the above algorithm, the element 'a' is inserted in a Queue and then NULL value shown as below: 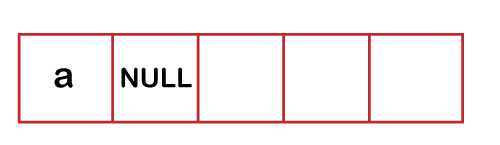
Then, the while loop will execute till the queue is not empty. In the 0th iteration, 'a' would be dequeued from the Queue. Now, 'p' points to the node 'a' and not equal to NULL, so it will print 'a' shown as below: 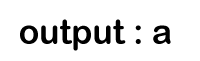
a->left is not NULL so enqueue(a->left) //b; queue would look like: 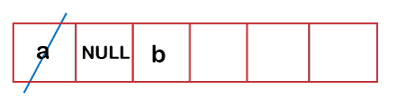
p = a ->right // c Since 'p' points to the node 'c', so the condition p != NULL becomes true and will print c. 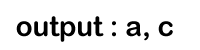
In the 1st iteration, 'p' is not equal to NULL; it is equal to 'c'. c->left is not equal to NULL // 'f'; so 'f' would be enqueued in a queue shown as below: 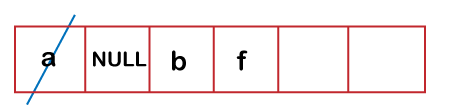
p = c-> right // 'g' Since 'p' points to the node 'g', so the condition p!= NULL becomes true and will print 'g'. 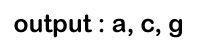
In the 2nd iteration, 'p' is not NULL; it is equal to 'g'. g->left is equal to NULL; so, condition p->left is false. p = g->right // 'l' Since 'p' points to the node 'l', so the condition p!= NULL becomes true and will print 'l'. 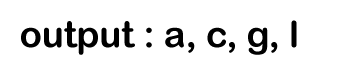
In the 3rd iteration, 'p' is not NULL; it is equal to 'l'. p-> left is not equal to NULL // 'm'; so 'm' would be enqueued in a queue shown as below: 
p = l->right // 'n' Since 'p' points to the node 'n', so the condition p != NULL becomes true and will print 'n' 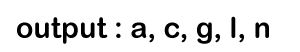
In the 4th iteration, 'p' is not equal to NULL; it is equal to 'n'. p->left is equal to NULL; so, the condition p->left is false. p =p->right; Since node 'n' does not have a right child so 'p' is equal to NULL. Now the condition p!= NULL is false, so the control comes out of the inner loop. The control moves to the outer loop, where we will check whether the queue is empty or not. Since the queue is not empty so control moves inside the loop, the element would be dequeued from the queue and now 'p' points to the node 'd'. In the 0th iteration, Since the p!= NULL so the condition becomes true of the inner loop. It will print 'b'. 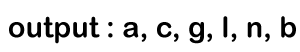
p->left is not equal to Null // 'd', so the condition p->left becomes true and it will enqueue 'd' in the queue shown as below: p = b->right // 'e' In the 1st iteration, the condition p!=NULL is true as 'p' points to the node 'e'. It will print 'e'. 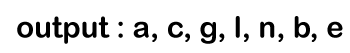
p-> left is equal to Null so the condition p->left becomes false. p = e->right //Since the node 'e' does not have a right child so 'p' contains NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is not empty so control inside the loop. Firstly, the element would be dequeued from the queue and now 'p' points to the node 'f'. In the 0th iteration, Since the p!= NULL so the condition becomes true of the inner loop. It will print 'f'. 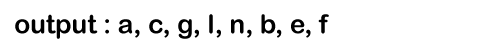
p-> left is not equal to NULL so the condition p-> left becomes true. p = f->right // 'k' In the 1st iteration, the condition p!= NULL is true as 'p' points to the node 'k'. It will print 'k'. 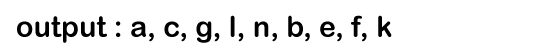
p-> left is equal to NULL so the condition p-> left becomes false. p = k-> right // Since the node 'k' does not have a right child so 'p' contains NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is not empty so control inside the loop. Firstly, the element would be dequeued from the queue and now 'p' points to the node 'm'. In the 0th iteration, Since the condition 'p!= NULL' is true so the control goes inside the inner loop. It will print 'm'. 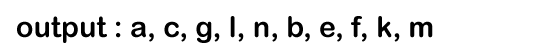
p-> left is equal to NULL so the condition p-> left becomes false. p = m -> right // Since the node 'm' does not have a right child, so 'p' contains NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is not empty so control inside the loop. Firstly, the element would be dequeued from the queue and now 'p' points to the node 'd'. In the 0th iteration, Since the condition p!= NULL is true, so control goes inside the loop. It will print 'd'. 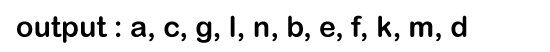
p-> left is not equal to NULL // 'h'; so, condition p->left is true and it will enqueue 'h' in a queue shown as below: p = d->right; // i; In the 1st iteration, Since the condition p!= NULL is true as 'p' points to the node 'i', so the control goes inside the loop. It will print 'i'. 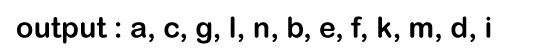
p-> left is equal to NULL as node 'i' does not have a left child, so condition p-> left becomes false. p = i->right; // Since node 'i' does not have a right child; therefore, 'p' points to NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is not empty so control inside the loop. Firstly, the element would be dequeued from the queue and now 'p' points to the node 'j'. In the 0th iteration, Since the condition p!= NULL is true as 'p' points to the node 'j', so control goes inside the loop. It will print 'j'. 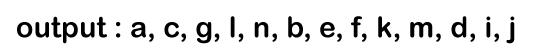
p->left is equal to NULL as node 'j' does not have a left child. p = j->right; Since the node 'j' does not have a right child so 'p' contains NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is not empty so control goes inside the loop. Firstly, the element would be dequeued from the queue and now 'p' points to the node 'h'. In the 0st iteration, Since the condition p!= NULL is true as 'p' points to the node 'h', so control goes inside the loop. It will print 'h'. 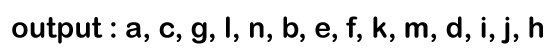
p->left is equal to NULL as node 'h' does not have a left child. p= h->right; Since the node 'h' does not have a right child, so 'p' contains the NULL value. Now the condition p!= NULL is false so the control comes out of the inner loop. The control moves to the outer loop where we will check whether the queue is empty or not. Since the queue is empty so control comes out of the outer the loop.
Next TopicVertical Traversal of a Binary tree
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









