DFS (Depth First Search) algorithm

In this article, we will discuss the DFS algorithm in the data structure. It is a recursive algorithm to search all the vertices of a tree data structure or a graph. The depth-first search (DFS) algorithm starts with the initial node of graph G and goes deeper until we find the goal node or the node with no children.

Because of the recursive nature, stack data structure can be used to implement the DFS algorithm. The process of implementing the DFS is similar to the BFS algorithm.

The step by step process to implement the DFS traversal is given as follows -

First, create a stack with the total number of vertices in the graph.
Now, choose any vertex as the starting point of traversal, and push that vertex into the stack.
After that, push a non-visited vertex (adjacent to the vertex on the top of the stack) to the top of the stack.
Now, repeat steps 3 and 4 until no vertices are left to visit from the vertex on the stack's top.
If no vertex is left, go back and pop a vertex from the stack.
Repeat steps 2, 3, and 4 until the stack is empty.

Applications of DFS algorithm

The applications of using the DFS algorithm are given as follows -

DFS algorithm can be used to implement the topological sorting.
It can be used to find the paths between two vertices.
It can also be used to detect cycles in the graph.
DFS algorithm is also used for one solution puzzles.
DFS is used to determine if a graph is bipartite or not.

Algorithm

Step 1: SET STATUS = 1 (ready state) for each node in G

Step 2: Push the starting node A on the stack and set its STATUS = 2 (waiting state)

Step 3: Repeat Steps 4 and 5 until STACK is empty

Step 4: Pop the top node N. Process it and set its STATUS = 3 (processed state)

Step 5: Push on the stack all the neighbors of N that are in the ready state (whose STATUS = 1) and set their STATUS = 2 (waiting state)

[END OF LOOP]

Step 6: EXIT

Pseudocode

DFS(G,v)   ( v is the vertex where the search starts )  
        Stack S := {};   ( start with an empty stack )  
        for each vertex u, set visited[u] := false;  
        push S, v;  
        while (S is not empty) do  
           u := pop S;  
           if (not visited[u]) then  
              visited[u] := true;  
              for each unvisited neighbour w of uu  
                 push S, w;  
           end if  
        end while  
     END DFS()  

Example of DFS algorithm

Now, let's understand the working of the DFS algorithm by using an example. In the example given below, there is a directed graph having 7 vertices.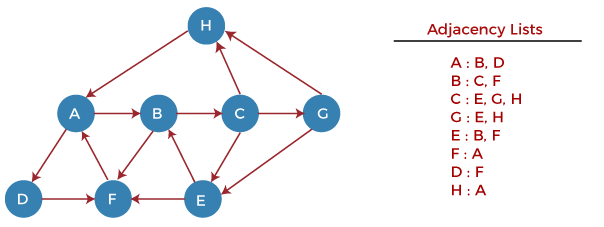

Now, let's start examining the graph starting from Node H.

Step 1 - First, push H onto the stack.

Step 2 - POP the top element from the stack, i.e., H, and print it. Now, PUSH all the neighbors of H onto the stack that are in ready state.

Step 3 - POP the top element from the stack, i.e., A, and print it. Now, PUSH all the neighbors of A onto the stack that are in ready state.

Print: A
STACK: B, D

Step 4 - POP the top element from the stack, i.e., D, and print it. Now, PUSH all the neighbors of D onto the stack that are in ready state.

Print: D
STACK: B, F

Step 5 - POP the top element from the stack, i.e., F, and print it. Now, PUSH all the neighbors of F onto the stack that are in ready state.

Print: F
STACK: B

Step 6 - POP the top element from the stack, i.e., B, and print it. Now, PUSH all the neighbors of B onto the stack that are in ready state.

Print: B
STACK: C

Step 7 - POP the top element from the stack, i.e., C, and print it. Now, PUSH all the neighbors of C onto the stack that are in ready state.

Print: C
STACK: E, G

Step 8 - POP the top element from the stack, i.e., G and PUSH all the neighbors of G onto the stack that are in ready state.

Print: G
STACK: E

Step 9 - POP the top element from the stack, i.e., E and PUSH all the neighbors of E onto the stack that are in ready state.

Print: E
STACK:

Now, all the graph nodes have been traversed, and the stack is empty.

Complexity of Depth-first search algorithm

The time complexity of the DFS algorithm is O(V+E), where V is the number of vertices and E is the number of edges in the graph.

The space complexity of the DFS algorithm is O(V).

Implementation of DFS algorithm

Now, let's see the implementation of DFS algorithm in Java.

In this example, the graph that we are using to demonstrate the code is given as follows -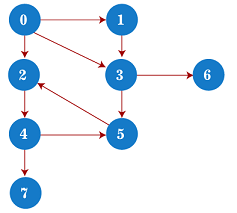

/*A sample java program to implement the DFS algorithm*/

import java.util.*;

class DFSTraversal {
  private LinkedList<Integer> adj[]; /*adjacency list representation*/
  private boolean visited[];

  /* Creation of the graph */
  DFSTraversal(int V) /*'V' is the number of vertices in the graph*/
  {
    adj = new LinkedList[V];
    visited = new boolean[V];

    for (int i = 0; i < V; i++)
      adj[i] = new LinkedList<Integer>();
  }

  /* Adding an edge to the graph */
  void insertEdge(int src, int dest) {
    adj[src].add(dest);
  }

  void DFS(int vertex) {
    visited[vertex] = true; /*Mark the current node as visited*/
    System.out.print(vertex + " ");

	Iterator<Integer> it = adj[vertex].listIterator();
    while (it.hasNext()) {
      int n = it.next();
      if (!visited[n])
        DFS(n);
    }
  }

  public static void main(String args[]) {
    DFSTraversal graph = new DFSTraversal(8);

        graph.insertEdge(0, 1);  
        graph.insertEdge(0, 2);  
        graph.insertEdge(0, 3);  
        graph.insertEdge(1, 3);  
        graph.insertEdge(2, 4);
        graph.insertEdge(3, 5);		
        graph.insertEdge(3, 6);  
        graph.insertEdge(4, 7);  
        graph.insertEdge(4, 5);  
        graph.insertEdge(5, 2);  
        
        System.out.println("Depth First Traversal for the graph is:");  
        graph.DFS(0);  
  }
}

Output

Conclusion

In this article, we have discussed the depth-first search technique, its example, complexity, and implementation in the java programming language. Along with that, we have also seen the applications of the depth-first search algorithm.

So, that's all about the article. Hope it will be helpful and informative to you.

Next TopicSpanning Tree

← prev next →