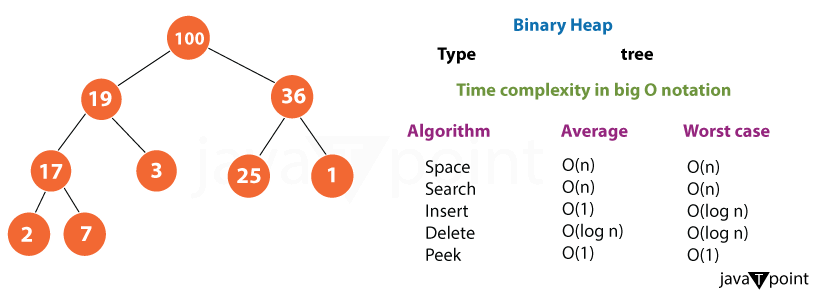
Time Complexity of using heap
A specialized tree-based data structure that complies with the heap property is called a heap. Programming and computer science applications of heaps include sorting algorithms and priority queues. There are primarily two kinds of heaps:
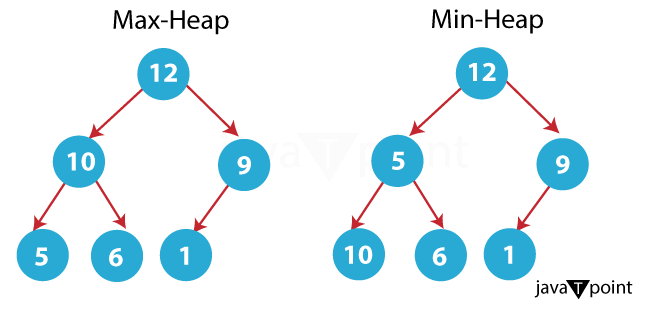
- Max Heap: A max heap is a set of nodes where the value of each node I is larger than or equal to the values of all of its offspring. This indicates that the largest element is located near the heap's base. Priority queues are frequently implemented using max heaps when the element with the highest priority is always at the front.
- Min Heap: In a min heap, the value of every given node I is either equal to or less than the values of all of its children. This indicates that the base of the heap is occupied by the smallest member. Among other things, priority queues can also be utilized with min heaps.
Usually, heaps are implemented as binary trees. In O(log n) time, where 'n' is the number of elements in the heap, binary heaps may efficiently handle insertion, deletion, and determining the minimum or maximum element.
Common use cases for heapsinclude:
- Priority Queues: Higher priority items are dequeued before lower priority elements in priority queues, which are frequently implemented using heaps.
- Heap Sort: Heap sort is an algorithm for comparison-based sorting that arranges elements in either ascending or descending order using a binary heap.
- Dijkstra's Algorithm: To determine the shortest path in weighted graphs, graph algorithms such as Dijkstra's algorithm employ heaps.
- Heap-based Data Structures: Binary search trees based on heaps are one example of the many data structures that may be built using heaps as their foundation.
- Memory Allocation: To effectively handle memory allocation and deallocation, some memory allocators make use of a heap data structure.
The time complexity of using a heap
Depending on the particular operation being carried out, a heap data structure's temporal complexity varies. The following are typical heap operations along with their temporal complexity:
- Insertion (heapify up): In the process of inserting a new element into a heap, it starts at the bottom and "bubbles up" or "percolates up" through the tree until the heap property is restored. This process is known as "heapify up." In most cases, the insertion time complexity is O(log n), where 'n' is the heap's element count. This is due to the heap's height having a logarithmic relationship with the number of elements.
- Deletion (Heapify Down): The final element in the heap is transferred to the root and "bubbles down" or "percolates down" through the tree to its correct location when the root element (such as the maximum element in a max heap or the minimum element in a min-heap) is removed. O(log n) is also the temporal complexity of deletion.
- Find Minimum/Maximum: Because the minimum or maximum value is always stored at the heap's root, determining the minimum element in a min-heap or the maximum element in a max heap is an O(1) operation.
- Heapify (Building a Heap): An array of components can be used to create a heap with O(n) time complexity. A bottom-up strategy is usually used for achieving this, beginning at the leaves and gradually "heapifying" subtrees.
- Heap Sort: The O(n log n) sorting algorithm known as "heap sort" is based on repeatedly extracting the element that represents the minimum (for a min heap) or maximum (for a max heap) and rebuilding the heap.
- Change Key (Update Key): Changing the value of a particular heap element requires either "heapify up" or "heapify down" operations, which have an O(log n) time complexity.
It is important to remember that these time complexities depend on the heap structure continuing to be balanced. Operations may become less complex in terms of time if the heap becomes unbalanced. Additionally, the choice of heap type can affect the real performance of your code because different heap types (e.g., binary heap, Fibonacci heap) may have slightly varying time complexity for specific operations.
Conclusion
In conclusion, heap data structures are essential to many computer science and programming applications because they provide effective means of organizing and working with data that has particular characteristics. The foundation for operations such as insertion, deletion, and identifying extremal elements, all with well-defined temporal complexity, is provided by max heaps and min heaps, each of which conforms to its own heap characteristics.
When designing an algorithm and selecting the best data structure for a given task, it is crucial to comprehend the temporal complications involved with heap operations. Although heaps are effective tools, choosing the right heap variant-such as a binary or Fibonacci heap-can also improve the efficiency of your code.
In conclusion, heaps are useful tools in the fields of computer science and programming because they are adaptable, effective data structures with a wide range of uses.
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









