Construct a linked list from 2D matrix

Understanding Linked Lists and Matrices

Linked Lists:

In the domain of computer science, the linked list emerges as an important data structure, containing a complexity that we often overlook. It arranges its elements, designating each as a "node." Unlike the known traits of arrays, linked lists represent an occasional presence upon their nodes, connected solely by complicated pointers.

Matrices:

A matrix, on the other hand, comes with two dimensions, enlisting rows and columns in in a way. It frequently serves as the base for tabular data, grids, and scenarios that demand careful structuring within a grid framework.

Matrix-to-Linked List Transformation:

Optimized Memory Consumption:

In a domain where memory efficiency works superior, matrices, particularly when it is full with null entries, demand a large allocation of memory resources. Similarly, linked lists stand for the efficiency by storing only the elements and their complicated connections.

Dynamic Operations:

The agility of linked lists comes to the fore when confronted with dynamic scenarios, offering an efficient arena for the seamless insertion and obliteration of elements. In the dynamic matrix universe, where elements oscillate in a rhythmic pattern of addition and subtraction, linked lists render an undeniable edge over their static matrix counterparts.

Reduced Space Complexity:

Transfiguring a matrix into a linked list results in a notable reduction in space complexity. By selectively working with the non-null elements within a linked list, a substantial part of memory finds itself freed, a transformation of significance in the domain of vast datasets and sparse matrices.

Sparse Matrix Representation:

In the domain of sparse matrices, the conversion to linked lists emerges as an artful change. This shift allows the user to optimize memory resources, creating a domain where efficiency and economy of storage guide further working.

Dynamic Data Structures:

The complicated flexibility of linked lists looks at a scenario where the size of the data structure has the liberty to work freely. In the matrix data, where the change is frequent, or when the sparse landscape demands memory optimization, the linked list helps the data.

Algorithms and Operations:

In the complicated set-up of algorithms and operations, the linked lists often work better than the others. This is especially true when the compilation involves frequent traversals and changes to matrix elements.

Steps to Transform Matrices into Linked Lists

1. Crafting the Node Masterpiece:

Start by forming a Node Class, the fundamental architecture of the made linked list. Each node, a chunk of data, possesses a complicated web of pointers, uniting them with their neighboring nodes, both in the same row and column.

2. Creating the Base:

Lay the cornerstone of an empty linked list and initiate the presence of a 'head,' the compass guiding this labyrinthine structure.

3. The Change of Iteration:

The transformation lies in the organized traversal of the 2D matrix. For every empty element that holds the matrix, birth a new node. Connect this new node with the existing nodes within the same row and column, which creates a balance.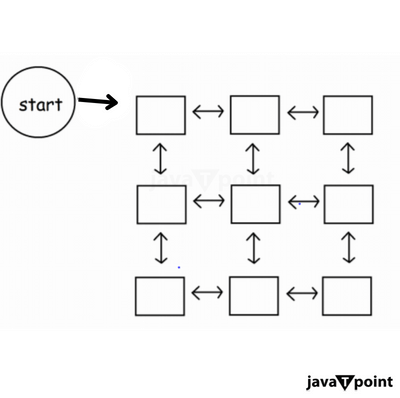

Code:

Output:

5 2 7 
8 9 3 
4 8 1

Advantages and Disadvantages of Linked Lists:

Advantages:

• Linked lists with the promise of swift additions and eliminations, their dynamic nature obviating the need for elaborate structural overhauls that arrays or lists often demand. They emerge as invaluable tools for the crafting of linear data structures.
• Inherent Freedom: Unlike their counterparts, linked lists defy the constraints of fixed or initial sizes, their chain-like structure affording them the luxury of adaptation.

Disadvantages:

• In the comparison against arrays, linked lists emerge as profligate consumers of memory resources. The mandatory inclusion of pointers, though essential, occupies extra space, leading to a trade-off.
• The quest for data in linked lists often unfolds at a slower pace, in stark contrast to the expeditious random access offered by arrays.