B Tree Properties

Traditional binary search trees have certain unpleasant limitations. Introducing the B-Tree, a versatile data structure that handles enormous quantities of data with ease. Traditional binary search trees can become unfeasible when it comes to storing and searching vast amounts of data because of their poor speed and high memory utilization. B-Trees, often referred to as Balanced Trees or B-Trees, are a kind of self-balancing tree that was created expressly to get around these restrictions.

B-Trees, also known as 'Big Key' trees, are distinguished from conventional binary search trees by the enormous number of keys that they can hold in a single node.

A B-Tree can have many keys at each node, which increases the branching factor and lowers the height of the tree. Because of the reduced disc I/O caused by this lower height, search and insertion operations are completed more quickly. Hard drives, flash memory, and CD-ROMs are examples of storage devices that benefit most from B-Trees because of their sluggish, clumsy data access.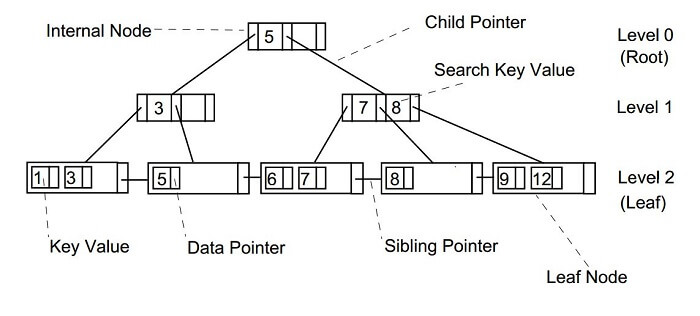

Each node in a B-Tree must have a minimum number of keys in order for the tree to remain balanced. No matter how the tree is initially shaped, this balance ensures that time complexity for operations like insertion, deletion, and searching is always O(log n).

B-Tree Time Complexity:

Here, the total number of elements in the B-tree is 'n'.

B-tree Properties:

• The leaves of a B-tree are all at the same level.
• The word minimal degree "t" defines a B-Tree. The size of a disc block determines the value of "t."
• There must be t-1 keys in every node besides the root. A root may have at least one key.
• At most (2*t - 1) keys may be present in any node, including the root.
• There are as many children in a node as there are keys, plus one.
• The keys of a node are organized in ascending order. The child between k1 and k2 contains each key in the range between k1 and k2.
• The B-Tree expands and contracts from the root, in contrast to the Binary Search Tree, which does not.
• The temporal complexity to search, insert, and remove is O, just like other balanced Binary Search Trees (log n).
• Only at the Leaf Node can a Node be inserted into a B-Tree.

NOTE:

The B-smallest Tree's possible height when there are n nodes and m children (the most children a node can have) is: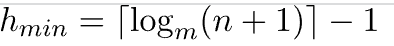

With n nodes and t being the smallest n umber of children, a non-root node can have, the greatest height of the B-Tree that can exist is: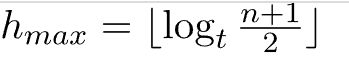

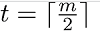
Origin of B Tree

• When brought into main memory (or RAM), data that has been saved on the disc in blocks is referred to as a data structure.
• Due to the large amount of data and frequent disc access, searching for a single record in a large volume of data necessitates reading the entire volume.
• To get around this, index tables that save the record references of the records based on the blocks they sit in are built. The amount of time and memory consumed is significantly decreased.
• We can develop multi-level index tables because we have a large amount of data.
• B Tree can be used to create multi-level indexes that keep the data sorted in a self-balancing way.
• B-Tree traversal is comparable to inorder Binary Tree traversal in terms of traversal. Starting with the leftmost child, we recursively print that child before doing the same for the keys and remaining children. At the end, recursively print the child on the right. A binary search tree and a B-tree both use similar search methods. The searchable key should be k.
• Recursively move up the tree, beginning at the root.
• If the non-leaf node has the key, we just return it for every visited node.
• If not, we go back to the node's proper child (the child that comes before the first greater key).
• If we arrive at a leaf node and k is not present there, return NULL.
• A binary tree search is similar to a B-Tree search. The algorithm uses recursion and is comparable. The search is optimized at each level so that if the key value is not present in the parent's range, it is present in a different branch. These numbers are also referred to as limiting values or separation values because they restrict the search. It will display NULL if we reach a leaf node and can't find the necessary key.

Why is a B-tree data structure necessary?

The demand for faster access to physical storage medium such a hard disc led to the development of B-tree. The secondary storage devices have a bigger capacity but are slower. These kinds of data structures, which reduce disc accesses, were required.

One key can only be stored in a node of another data structure, such as a binary search tree, AVL tree, red-black tree, etc. The height of such trees becomes very vast, and the access time increases if you need to store a lot of keys.

B-tree, on the other hand, can contain numerous child nodes and can store numerous keys in a single node. This causes the height to dramatically fall, enabling faster accesses of the disks.