B+ Tree Deletion

B-tree and B+ trees are typically used to achieve dynamic multilevel indexing. However, the disadvantage of the B-tree used for indexing is that it also keeps the data pointer (a pointer to the disc file block containing the key value), corresponding to a certain key value, in the B-tree node. This method significantly decreases the number of items that can fit inside a B-tree node, which leads to an increase in the B-level tree's structure and longer search times for records. By only storing data pointers at the tree's leaf nodes, the B+ tree gets rid of the above flaw.

As a result, the interior nodes of the B tree and the leaf nodes of a B+ tree have very distinct structures. It should be emphasized that since data pointers are only present at leaf nodes, all key values and their accompanying data pointers to the disc file block must be stored by leaf nodes for them to be accessible. Additionally, the leaf nodes are connected to offer organized access to the records. Therefore, the leaf nodes constitute the index's first level, with the internal nodes being the other levels in a multilevel index.

To only serve as a medium to regulate record searching, some of the leaf nodes' key values also appear in internal nodes. A B+ tree, unlike a B-tree, has two orders, "a" and "b," one for internal nodes and the other for external (or leaf) nodes. This is clear from the description above. An internal B+ tree of order "a" has the following node structure:

Each internal node has the following structure: where each Ki is a key-value pair and each Pi is a tree pointer (pointing to another node of the tree) (see diagram-I for reference).
Each internal node contains the following values for each search field: K1 < K2 < …. < Kc-1
The following statement is true for each value of search field "X" in the Pi-pointed subtree: Ki-1 < X <= Ki, where1 < i < c and, Ki-1 < X.
At most 'a' tree pointers are present in each internal node.
The internal nodes each have at least ceil(a/2) tree pointers, while the root node has at least two tree pointers.
An internal node has 'c -1' key values if it has 'c' pointers, where c< = a.

If the values are stored in order, most queries can be processed more quickly. However, it is impractical to expect to store the table's rows in sorted order and one after the other as doing so would necessitate recreating the table for each row that is added or removed.

This prompts us to think of putting our rows in a tree structure instead. Our initial thought would be a balanced binary search tree, like a red-black tree, but since databases are kept on disc, this actually doesn't make much sense. Disks function by reading and writing large blocks of data all at once; these blocks are typically 512 bytes or four kilobytes in size. A little portion of that is used by each node in a binary search tree,

Finding a structure that fits more neatly inside a disc block makes sense.

This results in the B+-tree, where each node contains up to d keys and up to d references to children. Each reference refers to the root of a subtree for which all values are between two of the node's keys and is therefore deemed to be "between" two of the node's keys.

Here is a somewhat small tree with the value 4 for d.

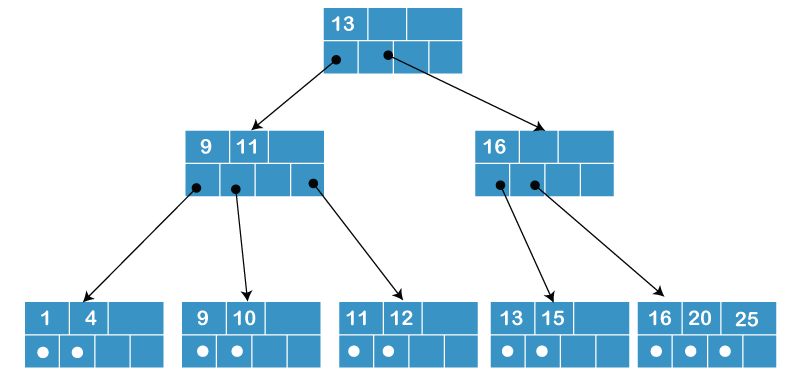
B+ tree characteristics:

Only leaf nodes can store data points.
Keys are found in internal nodes.
We utilize keys in B+ trees to perform direct element searches.
There will be at least "[m/2] -1" keys and a maximum of "m-1" keys if there are "m" elements.
At least two children and one key are present in the root node.
Each node other than the root can have a minimum of "m/2" children and a maximum of "m" children for "m" elements.

B+ Tree Deletion Process

B+ Tree deletion

In B+ Trees, deletion of a key involves several steps:

Search for the key to be deleted: Find the leaf node that contains the key to be deleted.
Remove the key: Remove the key-value pair from the leaf node. If the node has enough keys (minimum keys required to satisfy the B+ Tree property), no further action is required.
Adjust Tree Structure: If the leaf node has fewer keys than the minimum required, the node may need to be merged with a sibling node or have keys borrowed from a sibling node.
Update Index: If the key being deleted is an index key (i.e., located in an internal node), the index key may need to be updated to reflect the change in the tree structure.

In a B+ Tree, deletion is more complex than insertion, as the tree structure may need to be adjusted to maintain the B+ Tree properties. However, the search time for a key remains logarithmic, making B+ Trees an efficient data structure for indexing and searching large data sets.

C++ Program:

#include <bits/stdc++.h>

#include <iostream>
#include <random>
#include <utility>
#include <vector>

using namespace std;

class Node {
 public:
  Node(Node *parent = nullptr, bool isLeaf = false, Node *prev_ = nullptr,
       Node *next_ = nullptr)
      : parent(parent), isLeaf(isLeaf), prev(prev_), next(next_) {
    if (next_) {
      next_->prev = this;
    }

    if (prev_) {
      prev_->next = this;
    }
  }

  vector<int> keys;
  Node *parent;

  vector<Node *> children;
  vector<int> values;
  Node *next;
  Node *prev;

  bool isLeaf;

  int indexOfChild(int key) {
    for (int i = 0; i < keys.size(); i++) {
      if (key < keys[i]) {
        return i;
      }
    }
    return keys.size();
  }

  int indexOfKey(int key) {
    for (int i = 0; i < keys.size(); i++) {
      if (key == keys[i]) {
        return i;
      }
    }
    return -1;
  }

  Node *getChild(int key) { return children[indexOfChild(key)]; }

  void setChild(int key, vector<Node *> value) {
    int i = indexOfChild(key);
    keys.insert(keys.begin() + i, key);
    children.erase(children.begin() + i);
    children.insert(children.begin() + i, value.begin(), value.end());
  }

  tuple<int, Node *, Node *> splitInternal() {
    Node *left = new Node(parent, false, nullptr, nullptr);
    int mid = keys.size() / 2;

    copy(keys.begin(), keys.begin() + mid, back_inserter(left->keys));
    copy(children.begin(), children.begin() + mid + 1,
         back_inserter(left->children));

    for (Node *child : left->children) {
      child->parent = left;
    }

    int key = keys[mid];
    keys.erase(keys.begin(), keys.begin() + mid + 1);
    children.erase(children.begin(), children.begin() + mid + 1);

    return make_tuple(key, left, this);
  }

  int get(int key) {
    int index = -1;
    for (int i = 0; i < keys.size(); ++i) {
      if (keys[i] == key) {
        index = i;
        break;
      }
    }

    if (index == -1) {
      cout << "key " << key << " not found" << endl;
    }

    return values[index];
  }

  void set(int key, int value) {
    int i = indexOfChild(key);
    if (find(keys.begin(), keys.end(), key) == keys.end()) {
      keys.insert(keys.begin() + i, key);
      values.insert(values.begin() + i, value);
    } else {
      values[i - 1] = value;
    }
  }

  tuple<int, Node *, Node *> splitLeaf() {
    Node *left = new Node(parent, true, prev, this);
    int mid = keys.size() / 2;

    left->keys = vector<int>(keys.begin(), keys.begin() + mid);
    left->values = vector<int>(values.begin(), values.begin() + mid);

    keys.erase(keys.begin(), keys.begin() + mid);
    values.erase(values.begin(), values.begin() + mid);

    return make_tuple(keys[0], left, this);
  }
};

class BPlusTree {
 public:
  BPlusTree(int _maxCapacity = 4) {
    root = new Node(nullptr, true, nullptr, nullptr);
    maxCapacity = _maxCapacity > 2 ? _maxCapacity : 2;
    minCapacity = maxCapacity / 2;
    depth = 0;
  }

  Node *root;
  int maxCapacity;
  int minCapacity;
  int depth;

  Node *findLeaf(int key) {
    Node *node = root;
    while (!node->isLeaf) {
      node = node->getChild(key);
    }
    return node;
  }

  int get(int key) { return findLeaf(key)->get(key); }

  void set(int key, int value) {
    Node *leaf = findLeaf(key);
    leaf->set(key, value);
    if (leaf->keys.size() > maxCapacity) {
      insert(leaf->splitLeaf());
    }
  }

  void insert(tuple<int, Node *, Node *> result) {
    int key = std::get<0>(result);
    Node *left = std::get<1>(result);
    Node *right = std::get<2>(result);
    Node *parent = right->parent;
    if (parent == nullptr) {
      left->parent = right->parent = root =
          new Node(nullptr, false, nullptr, nullptr);
      depth += 1;
      root->keys = {key};
      root->children = {left, right};
      return;
    }
    parent->setChild(key, {left, right});
    if (parent->keys.size() > maxCapacity) {
      insert(parent->splitInternal());
    }
  }

  void removeFromLeaf(int key, Node *node) {
    int index = node->indexOfKey(key);
    if (index == -1) {
      cout << "Key " << key << " not found! Exiting ..." << endl;
      exit(0);
    }
    node->keys.erase(node->keys.begin() + index);
    node->values.erase(node->values.begin() + index);
    if (node->parent) {
      int indexInParent = node->parent->indexOfChild(key);
      if (indexInParent)
        node->parent->keys[indexInParent - 1] = node->keys.front();
    }
  }

  void removeFromInternal(int key, Node *node) {
    int index = node->indexOfKey(key);
    if (index != -1) {
      Node *leftMostLeaf = node->children[index + 1];
      while (!leftMostLeaf->isLeaf)
        leftMostLeaf = leftMostLeaf->children.front();

      node->keys[index] = leftMostLeaf->keys.front();
    }
  }

  void borrowKeyFromRightLeaf(Node *node, Node *next) {
    node->keys.push_back(next->keys.front());
    next->keys.erase(next->keys.begin());
    node->values.push_back(next->values.front());
    next->values.erase(next->values.begin());
    for (int i = 0; i < node->parent->children.size(); i++) {
      if (node->parent->children[i] == next) {
        node->parent->keys[i - 1] = next->keys.front();
        break;
      }
    }
  }

  void borrowKeyFromLeftLeaf(Node *node, Node *prev) {
    node->keys.insert(node->keys.begin(), prev->keys.back());
    prev->keys.erase(prev->keys.end() - 1);
    node->values.insert(node->values.begin(), prev->values.back());
    prev->values.erase(prev->values.end() - 1);
    for (int i = 0; i < node->parent->children.size(); i++) {
      if (node->parent->children[i] == node) {
        node->parent->keys[i - 1] = node->keys.front();
        break;
      }
    }
  }

  void mergeNodeWithRightLeaf(Node *node, Node *next) {
    node->keys.insert(node->keys.end(), next->keys.begin(), next->keys.end());
    node->values.insert(node->values.end(), next->values.begin(),
                        next->values.end());
    node->next = next->next;
    if (node->next) node->next->prev = node;
    for (int i = 0; i < next->parent->children.size(); i++) {
      if (node->parent->children[i] == next) {
        node->parent->keys.erase(node->parent->keys.begin() + i - 1);
        node->parent->children.erase(node->parent->children.begin() + i);

        break;
      }
    }
  }

  void mergeNodeWithLeftLeaf(Node *node, Node *prev) {
    prev->keys.insert(prev->keys.end(), node->keys.begin(), node->keys.end());
    prev->values.insert(prev->values.end(), node->values.begin(),
                        node->values.end());

    prev->next = node->next;
    if (prev->next) prev->next->prev = prev;

    for (int i = 0; i < node->parent->children.size(); i++) {
      if (node->parent->children[i] == node) {
        node->parent->keys.erase(node->parent->keys.begin() + i - 1);
        node->parent->children.erase(node->parent->children.begin() + i);
        break;
      }
    }
  }

  void borrowKeyFromRightInternal(int myPositionInParent, Node *node,
                                  Node *next) {
    node->keys.insert(node->keys.end(), node->parent->keys[myPositionInParent]);
    node->parent->keys[myPositionInParent] = next->keys.front();
    next->keys.erase(next->keys.begin());
    node->children.insert(node->children.end(), next->children.front());
    next->children.erase(next->children.begin());
    node->children.back()->parent = node;
  }

  void borrowKeyFromLeftInternal(int myPositionInParent, Node *node,
                                 Node *prev) {
    node->keys.insert(node->keys.begin(),
                      node->parent->keys[myPositionInParent - 1]);
    node->parent->keys[myPositionInParent - 1] = prev->keys.back();
    prev->keys.erase(prev->keys.end() - 1);
    node->children.insert(node->children.begin(), prev->children.back());
    prev->children.erase(prev->children.end() - 1);
    node->children.front()->parent = node;
  }

  void mergeNodeWithRightInternal(int myPositionInParent, Node *node,
                                  Node *next) {
    node->keys.insert(node->keys.end(), node->parent->keys[myPositionInParent]);
    node->parent->keys.erase(node->parent->keys.begin() + myPositionInParent);
    node->parent->children.erase(node->parent->children.begin() +
                                 myPositionInParent + 1);
    node->keys.insert(node->keys.end(), next->keys.begin(), next->keys.end());
    node->children.insert(node->children.end(), next->children.begin(),
                          next->children.end());
    for (Node *child : node->children) {
      child->parent = node;
    }
  }

  void mergeNodeWithLeftInternal(int myPositionInParent, Node *node,
                                 Node *prev) {
    prev->keys.insert(prev->keys.end(),
                      node->parent->keys[myPositionInParent - 1]);
    node->parent->keys.erase(node->parent->keys.begin() + myPositionInParent -
                             1);
    node->parent->children.erase(node->parent->children.begin() +
                                 myPositionInParent);
    prev->keys.insert(prev->keys.end(), node->keys.begin(), node->keys.end());
    prev->children.insert(prev->children.end(), node->children.begin(),
                          node->children.end());
    for (Node *child : prev->children) {
      child->parent = prev;
    }
  }

  void remove(int key, Node *node = nullptr) {
    if (node == nullptr) {
      node = findLeaf(key);
    }
    if (node->isLeaf) {
      removeFromLeaf(key, node);
    } else {
      removeFromInternal(key, node);
    }

    if (node->keys.size() < minCapacity) {
      if (node == root) {
        if (root->keys.empty() && !root->children.empty()) {
          root = root->children[0];
          root->parent = nullptr;
          depth -= 1;
        }
        return;
      }

      else if (node->isLeaf) {
        Node *next = node->next;
        Node *prev = node->prev;

        if (next && next->parent == node->parent &&
            next->keys.size() > minCapacity) {
          borrowKeyFromRightLeaf(node, next);
        } else if (prev && prev->parent == node->parent &&
                   prev->keys.size() > minCapacity) {
          borrowKeyFromLeftLeaf(node, prev);
        } else if (next && next->parent == node->parent &&
                   next->keys.size() <= minCapacity) {
          mergeNodeWithRightLeaf(node, next);
        } else if (prev && prev->parent == node->parent &&
                   prev->keys.size() <= minCapacity) {
          mergeNodeWithLeftLeaf(node, prev);
        }
      } else {
        int myPositionInParent = -1;

        for (int i = 0; i < node->parent->children.size(); i++) {
          if (node->parent->children[i] == node) {
            myPositionInParent = i;
            break;
          }
        }

        Node *next;
        Node *prev;

        if (node->parent->children.size() > myPositionInParent + 1) {
          next = node->parent->children[myPositionInParent + 1];
        } else {
          next = nullptr;
        }

        if (myPositionInParent) {
          prev = node->parent->children[myPositionInParent - 1];
        } else {
          prev = nullptr;
        }

        if (next && next->parent == node->parent &&
            next->keys.size() > minCapacity) {
          borrowKeyFromRightInternal(myPositionInParent, node, next);
        }

        else if (prev && prev->parent == node->parent &&
                 prev->keys.size() > minCapacity) {
          borrowKeyFromLeftInternal(myPositionInParent, node, prev);
        }

        else if (next && next->parent == node->parent &&
                 next->keys.size() <= minCapacity) {
          mergeNodeWithRightInternal(myPositionInParent, node, next);
        }

        else if (prev && prev->parent == node->parent &&
                 prev->keys.size() <= minCapacity) {
          mergeNodeWithLeftInternal(myPositionInParent, node, prev);
        }
      }
    }
    if (node->parent) {
      remove(key, node->parent);
    }
  }

  void print(Node *node = nullptr, string _prefix = "", bool _last = true) {
    if (!node) node = root;
    cout << _prefix << "? [";
    for (int i = 0; i < node->keys.size(); i++) {
      cout << node->keys[i];
      if (i != node->keys.size() - 1) {
        cout << ", ";
      }
    }
    cout << "]" << endl;

    _prefix += _last ? "   " : "?  ";

    if (!node->isLeaf) {
      for (int i = 0; i < node->children.size(); i++) {
        bool _last = (i == node->children.size() - 1);
        print(node->children[i], _prefix, _last);
      }
    }
  }
};

int main() {
  BPlusTree tree(3);
  vector<int> random_list = {5,  9,  1,  3,   4,   59,  65,  45,
                             89, 29, 68, 108, 165, 298, 219, 569,
                             37, 47, 53, 6,   43,  51,  57,  49};

  vector<int> random_list_2 =
      vector<int>(random_list.begin(), random_list.end());

  for (int r : random_list_2) {
    for (int i : random_list) {
      cout << endl << "-------------" << endl;
      cout << "Inserting " << i << endl << endl;
      cout << "-------------" << endl << endl;

      tree.set(i, i);
      tree.print();
    }

    cout << endl << "-------------------------" << endl;
    cout << "All keys are inserted ..." << endl;
    cout << "-------------------------" << endl << endl;

    tree.print();

    shuffle(random_list.begin(), random_list.end(), default_random_engine(r));
    for (int i : random_list) {
      tree.remove(i);
      cout << endl << "-------------" << endl;
      cout << "Removing " << i << endl;
      cout << "-------------" << endl << endl;
      tree.print();
    }
  }

  return 0;
}

Output

Explanation:

This code uses a self-balancing tree data structure called a B+ tree, which is frequently used in databases to store and retrieve data quickly. It is comparable to a binary search tree, but each node can store numerous keys and have more than two children.

Class Node

A Node in the B+ tree is represented by the Node class. Its numerous member factors include:

The keys found in the node are stored in a vector of integers called keys.
parent is a pointer to the parent node of the present node.
Children is a vector containing pointers to the present node's child nodes. Only when the present node is not a leaf node is this used.
The numbers connected to the node's keys are stored in a vector of integers called values. Only when the present node is a leaf node is this used.
The terms "next" and "prev" refer to the tree's next and previous branches, respectively. In order to facilitate effective range queries, this is used to build a linked list of leaf nodes. (not implemented though).
The boolean value isLeaf shows whether or not the current node is a leaf node.

The Node class has several member functions:

Node(Node *parent = nullptr, bool isLeaf = false, Node *prev_ = nullptr, Node *next_ = nullptr) is the constructor for the Node class. It takes four optional arguments: a pointer to the parent node, a boolean indicating whether the node is a leaf or not, and pointers to the previous and next nodes in the tree. If the prev and next arguments are provided, it updates the linked list pointers accordingly.
indexOfChild(int key) gives the child node's index, which contains the specified key. The index at which the key would be added is returned if the key is not present in the node.
The function indexOfKey(int key) gives the position of the specified key in the keys vector. It gives -1 if the key cannot be located.
The result value of getChild(int key) is a pointer to the child node that contains the specified key.
setChild(int key, vector value) places the specified key and a vector of child nodes at the proper location in the keys and children vectors.
splitInternal() is used to split an internal node when it becomes full. Half of the keys and offspring are transferred to the new node, which is also given a new node. It gives a tuple with a pointer to the left node, a pointer to the right node, and the key that will be inserted into the parent node.
get(int key) gives the value corresponding to the supplied key. If the key cannot be located, an error notice is printed.
The set(int key, int value) function places the specified key and value at the proper location in the keys and values arrays. Updates are made to the related value if the key is already present.
When an internal component becomes, splitInternal() is utilised to divide it.
When a leaf node fills up, the splitLeaf() function is used to divide it. Half of the names and values are transferred to the new node, which is also created. It gives a tuple with a pointer to the left node, a pointer to the right node, and the key that will be inserted into the parent node.
When one of the leaf nodes becomes underfull, merge(Node* sibling) is used to combine the two leaf nodes. It updates the linked list pointers and transfers all the names and values from the sibling node to the current node.

BPlusTree class:

A B+ tree data structure is represented by the BPlusTree class. Its numerous member factors include:

root: a pointing device to the tree's base node.
maxCapacity: an integer that represents the most keys a node can have before having to be divided.
minCapacity: an integer showing the bare minimum number of keys a node can hold before being deemed under full and potentially needing to merge with another node or borrow a key from a neighboring node.
depth: a number that represents the tree's depth.

There are several member methods in the BPlusTree class.

BPlusTree(int _maxCapacity = 4) is the constructor for the BPlusTree class. It takes an optional argument _maxCapacity which specifies the maximum number of keys that a node can have before it needs to be split. If _maxCapacity is not provided, the default value of 4 is used. The constructor creates a new root node and initializes the maxCapacity, minCapacity, and depth member variables.
The function Node* findLeaf(int key) returns a pointer to the leaf node that contains the provided key. It moves down the tree from the root node until it hits a leaf node.
The function int get(int key) returns the number related to the specified key. It uses the findLeaf function to find the leaf node that contains the key before using the get function to get the value.
The void set() function adds the specified property and value to the tree. The key and value are inserted by calling the leaf node's set function after calling the findLeaf method to identify the leaf node where the key would be stored. If the leaf node becomes full as a result, it calls the insert function to split the node.
The outcomes of a node split are inserted into the tree using the void insert(tuple result) function. It requires a tuple that includes pointers to the left and right child nodes as well as the value that will be inserted into the parent node. In order to make a new root node and update the root and depth member variables, it first determines whether the parent node is null. If not, it uses the parent node's setChild function to put the key and child nodes in the proper places. In the event that the parent node fills up, it splits the parent node by invoking the insert method repeatedly.
The void remove(int key) function eliminates the specified key from the tree. It uses the findLeaf function to find the leaf node that contains the key before using the removeFromLeaf function to get the key out of that leaf node. If consequently the leaf node becomes underfull, it determines whether it needs to merge with a neighboring node or if it has a neighboring node with spare keys that it can borrow from. The root node is updated to point to the lone surviving child if the node is the root node and empty as a consequence of the removal.
The void removeFromLeaf(int key, Node *node) function takes a key and eliminates it from a leaf node. It updates the key in the parent node if required and removes the key and related value from the keys and values vectors.
The void removeFromInternal(int key, Node *node) function removes the specified key from the specified internal node . If the key is present in the keys vector, the smallest key from the rightmost child is used to substitute it. If the internal node is consequently under full, it determines whether it can borrow keys from a nearby node that has spares or whether it needs to merge with a neighboring node.
The void function borrowKeyFromRightLeaf(Node *node, Node *next) obtains a key from the leaf node's right neighbour. It removes the key and value from the right neighbor and adds the first key and value from that neighbor to the provided node. If necessary, it additionally updates the key in the right neighbor's parent node.
The void function borrowKeyFromLeftLeaf(Node *node, Node *prev) takes a key from the leaf node's left neighbor. It removes the key and value from the left neighbor and adds the last key and value from the left neighbor to the provided node. If necessary, it additionally updates the key in the parent node of the provided node.
void mergeNodeWithRightLeaf(Node *node) joins the supplied node with its right neighbour. It updates the linked list pointers and appends the keys and values from the right neighbour to the specified node. The appropriate neighbour node is then deleted.
The void function mergeNodeWithLeftLeaf(Node *node) joins the specified node with its left neighbour. The linked list pointers are updated, and the keys and values from the left neighbour are inserted at the start of the keys and values vectors in the specified node. Next, the left neighbour node is deleted.
The void function borrowKeyFromRightInternal(Node *node) obtains a key from the internal node's right neighbour. It removes the key and child from the right neighbour and puts the first key and child from the right neighbour into the specified node.It also updates the key in the parent node of the right neighbor if necessary.
The void function borrowKeyFromLeftInternal(Node *node) takes a key from the internal node's left neighbour.

The final key and child from the left neighbour are removed, and they are inserted into the specified node.

If necessary, it additionally updates the key in the parent node of the provided node.

The void function mergeNodeWithRightInternal(Node *node) joins the internal node with the right neighbour. It modifies the key in the parent node if necessary and appends the keys and children from the appropriate neighbour to the specified node.

The appropriate neighbour node is then deleted.

The void function mergeNodeWithLeftInternal(Node *node) joins the internal node with the left neighbour.It inserts the keys and children from the left neighbour at the beginning of the keys and children vectors.

Advantages of B+ Trees:

In comparison to a B-tree with the same number of levels, a B+ tree can store more entries in its internal nodes. This emphasizes how much the search time for every specific key has been improved. Because of their lower levels and Pnext pointers, B+ trees are particularly rapid and effective at accessing records from drives.
A B+ tree allows for both sequential and direct access to data.
To fetch records, an equivalent number of disc accesses are required.
Because of the redundant search keys in B+ trees, it is impossible to store search keys again.

Disadvantages of B+ Trees:

The difficulty of accessing the keys in a sequential manner is the main disadvantage of B-tree. The quick random access is still present in the B+ tree.

Application of B+ Trees:

Multiple Indexing
faster tree operations (insertion, deletion, search)
indexing a database

B Tree Vs B+ Tree

The following are some of the variations between B and B+ tree:

Data and search keys are kept in internal or leaf nodes in a B tree. Data, however, is only kept at leaf nodes of the B+ tree.
Because all data are located in leaf nodes of a B+ tree, searching for any data is incredibly simple. Data cannot be discovered in leaf nodes of a B tree.
Data can be located in internal nodes or leaf nodes of a B tree. Internal node deletion is highly challenging. Data only exists in leaf nodes of a B+ tree. Leaf node deletion is fairly simple because it can be directly deleted.
Insertion in B tree is more complicated than B+ tree.
B+ trees store redundant search key but B tree has no redundant value.
In a B+ tree, leaf nodes data are ordered as a sequential linked list but in B tree the leaf node cannot be stored using a linked list. Many database systems' implementations prefer the structural simplicity of a B+ tree.

The basic difference lies between how they make use of the internal storage.

Overview:

A B+ tree is a non-linear storage structure that stores a collection of data elements with a "one-to-many" relationship, typically used in databases and operating system file systems.

Non-leaf nodes do not store data, only indexes (redundant), and more indexes can be placed.
Leaf nodes contain all index fields.
Leaf nodes are linked with pointers to improve interval access performance;

Why B+ Tree?

Since MySQL usually stores data on disk, reading data will generate disk IO consumption. The non-leaf nodes of the B+ tree do not store data. Usually, the size of a node is set to the size of the disk page, so that each node of the B+ tree can put more keys, and the height of the B+ tree is lower, reducing disk IO consumption.
B+ tree leaf nodes form a linked list and use range search and sorting.

MySQL uses B+ tree as an index.

Since MySQL usually stores data on disk, reading data will generate disk IO consumption. The non-leaf nodes of the B+ tree do not save data, but the non-leaf nodes of the B tree will save data. Usually, the size of a node will be set to the disk page size, so that each node of the B+ tree can hold more keys, while the B tree has more keys. few. As a result, the height of the B tree will be higher than that of the B+ tree, which will result in more disk IO consumption.
B+ tree leaf nodes form a linked list and use range search and sorting. The B-tree for range search and sorting requires recursive traversal of the tree.

B+ tree time complexity

Best Case Complexity of Time

The searching operation in a B+ tree has the same best case time complexity as the deleting operation in a B+ tree. Therefore, the B+ tree deletion's best case time complexity is O(logn)

Average Case Time Complexity

B+ trees have an average case time complexity of O(logn). The B+ tree's deletion technique uses the same amount of time as the search process. So both search and deletion will take the same amount of time.

Worst Case Time Complexity

B+ trees have a worst-case temporal complexity of O(logn).

B+ tree space complexity

In a B+ tree, the worst-case space complexity and average space complexity are both identical.

The average and the best space complexity is O(n)

Next TopicB+ Tree Insertion

← prev next →