Count of Valid Splits in a String

Problem Statement

Given a string s, you are tasked with determining the count of valid splits. A split is deemed valid if you can divides into two nonempty substrings, s_first and s_second, such that their combination equals s (i.e., s_first + s_second = s), and both substrings have an identical set of distinct letters.

Find the number of valid splits that can be formed in string s.

Java Implementation

Java Approach 1 Using HashMaps

import 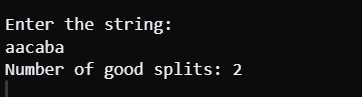java. util.HashMap;
import java. util.Scanner;
public class SplitString {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("Enter the string: ");
        String s = scanner.nextLine();
        int result = numSplits(s);
        System.out.println("Number of good splits: " + result);
        scanner.close();
    }
    public static int numSplits(String s) {
        HashMap<Character, Integer> left = new HashMap<>();
        HashMap<Character, Integer> right = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            right.put(s.charAt(i), right.getOrDefault(s.charAt(i), 0) + 1);
        }
        int count = 0; 
        for (int i = 0; i < s.length(); i++) {
            char curr = s.charAt(i); 
            left.put(curr, left.getOrDefault(curr, 0) + 1); 
            right.put(curr, right.getOrDefault(curr, 0) - 1); 
            if (right.get(curr) <= 0) {   
                right.remove(curr);
            }
            if (left.size() == right.size()) {   
                count++;
            }
        }
        return count;
    }
}

Output:

Code Explanation:

This Java code aims to resolve the problem of finding the number of good splits for a string s. A good split occurs when s becomes sleft concatenated with sright so as to have an equivalent resultant string which is sleft+sright=s. Also, sleft should contain the same count of unique letters as sright should do.

To achieve this, the code employs two HashMaps: left and right. It maintains counts for each character appearing at both ends of the string in these HashMaps. At the beginning, the algorithm scans through the string and populates it in the right HashMap with instances of characters therein.

The code iterates through the string a second time and updates the left HashMap with each character encountered. At the same time, it draws away from the right HashMap, performing an opposite action to that in which figures are switched from the right to left sides. The count of a character is removed from the HashMap once its count on the right side becomes zero or negative.

At each stage, this code verifies if there are as many types of distinct figures in one array as they occur in another. Then, it increases the count as a valid split. The process involves comparing the sizes of the left and right HashMaps.

Time Complexity:

Time complexity is O(N), and N represents the length of the input string. A single pass on the string while putting get and remove operations at Hash Maps are constant time. Therefore, the overall time complexity is O(N).

Space Complexity:

For example, the space complexity is O(K) for a single K-character alphabet. In the worst scenario where all alphabets are different, it can be noted that one hash map might expand up to k. Space requirement for hashing map increases proportionally to the alphabets, and hence, the spatial complexity is of the order of unique characters in the message, which makes the result

Java Approach 2 Using HashSet

import 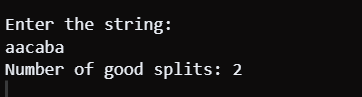java. util.HashSet;
import java. util.Scanner; 
public class GoodSplitsCounter {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);    
        System.out.println("Enter the string:");
        String s = scanner.nextLine();
        int result = countGoodSplits(s); 
        System.out.println("Number of good splits: " + result); 
        scanner.close();
    }
    public static int countGoodSplits(String s) {
        HashSet<Character> leftDistinct = new HashSet<>();
        int[] leftDistinctCount = new int[s.length()];
        HashSet<Character> rightDistinct = new HashSet<>();
        int[] rightDistinctCount = new int[s.length()];
        for (int i = 0; i < s.length(); i++) {
            leftDistinct.add(s.charAt(i)); 
            leftDistinctCount[i] = leftDistinct.size();
        }
        rightDistinct.add(s.charAt(s.length() - 1));  
        rightDistinctCount[s.length() - 1] = 1;
        for (int i = s.length() - 2; i >= 0; i--) {
            rightDistinct.add(s.charAt(i));    
            rightDistinctCount[i] = rightDistinct.size();
        }

        int goodSplits = 0;
        for (int i = 1; i < s.length(); i++) {
            if (leftDistinctCount[i - 1] == rightDistinctCount[i]) {
                goodSplits++;
            }
        }
        return goodSplits;
    }
}

Output:

Code Explanation:

Here, I define a good split as being when one can separate the string s and be able to create two strings, s_{left} and s_{right}. These must be nonempty, where s_{left}+s_{right}=s, and must also result in an improved metric value compared to that. Moreover, both strings must contain the same number of different characters and should not have any missing characters.

It has two HashSet objects called leftDistinct and rightDistent to store unique letters from both sides. These variables are leftDistinctCount, which keeps track of all distinct characters per position in each array, while rightDistinctCount also does this from left to right.

The algorithm begins by traversing the string from left to right, adding items to the leftDistinct set, and incrementing values in the leftDistinctCount array. Likewise, it proceeds from the right side to the left, incrementally adjusting the rightDistinct and rightDistinctCount array.

Lastly, the code then compares the number of unique characters on each side in the same position. It increases the goodSplits when the counts agree. Therefore, it becomes the sum of all possible positions in which the string is segmented into two equal parts having the same kind of unique letters.

Time Complexity:

For an input string s, a solution having a time complexity of O(N) is constructed using both left-to-right and right-to-left traverse directions.

Space Complexity:

The space complexity is O(N). Space is required to create HashSet objects (leftDistinct and rightDistinct) and arrays (leftDistinctCount and rightDistinctCount), both proportional in size based on the length of the input string.

Java Approach 3 Using Two Pointer

import 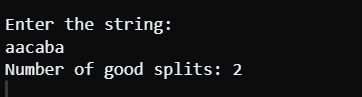java. util.HashSet;
import java. util.Scanner;
import java. util.Set;
public class GoodSplitsCounter {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("Enter the string:");
        String s = scanner.nextLine();
        int result = countGoodSplits(s); 
        System.out.println("Number of good splits: " + result); 
        scanner.close();
    }
    public static int countGoodSplits(String s) {
        if (s.length() == 0 || s.length() == 1)
            return 0;
        int size = s.length();
        int[] leftDistinctCount = new int[size];
        int[] rightDistinctCount = new int[size]; 
        Set<Character> charSet = new HashSet<>();
        // Count distinct characters from the left side  
        leftDistinctCount[0] = 1;
        charSet.add(s.charAt(0));
        for (int i = 1; i < size; i++) {
            char c = s.charAt(i);
            if (charSet.add(c))   
                leftDistinctCount[i] = leftDistinctCount[i - 1] + 1;
            else   
                leftDistinctCount[i] = leftDistinctCount[i - 1];
        }
        // Count distinct characters from the right side
        charSet = new HashSet<>();
        charSet.add(s.charAt(size - 1)); 
        rightDistinctCount[size - 1] = 1;
        for (int i = size - 2; i >= 0; i--) {
            char c = s.charAt(i);
            if (charSet.add(c))   
                rightDistinctCount[i] = rightDistinctCount[i + 1] + 1;
            else   
                rightDistinctCount[i] = rightDistinctCount[i + 1];
        }
        int count = 0, i = 0, j = 1;
        // Compare positions where the distinct count is the same
        while (i < size && j < size) {
            if (leftDistinctCount[i] == rightDistinctCount[j]) 
                count++;
                i++;
                j++;
        }
        return count;
    }
}

Output:

Code Explanation:

This Java code would count how many valid splits there are in string s where, at each good split, you get two nonempty substrings left and right, such that (left + right) equals s. Secondly, there should be an equal number of unique letters in both substrings.

LeftDistinctCount and rightDistinctCount are stored in an array. It helps identify unique characters by using a HashSet called charSet.

For starters, the program checks if the length of the string is zero or one; if so, it returns 0. After that, it counts up distinct characters using a left-to-right and right-to-left sweep.

Lastly, it compares the number of unique characters on either side with their respective match location. It adds the count if the number of matches is right. The end product is the sum of all positions in which the string might be separated evenly by its nonrepeated letters.

Time Complexity:

The solution has a time complexity of, at most, O(N) where N =string length|. This means both traversals have the same linear time complexity.

Space Complexity:

The space complexity is O(N). Space is computed based on the input string length for the arrays (leftDistinctCount and rightDistinctCount), as well as the unique characters in charSet.

Conclusion:

The algorithm efficiently calculates the number of good splits in a given string, where a good split involves dividing the string into two non-empty substrings with equal counts of distinct characters. By employing two arrays and a HashSet, it navigates the string from both ends, keeping track of distinct character counts. The solution demonstrates a time complexity of O(N) and a space complexity of O(N). For an input like "aacaba," the code successfully identifies and counts the valid splits, providing a robust solution to the problem.

Next TopicDelete all occurrences of a given key in a linked list

← prev next →