DS Tutorial
DS Array
DS Linked List
Linked List
Types of Linked List
Singly Linked List
Doubly Linked List
Circular Linked List
Circular Doubly List
Skip list in DS
DS Stack
DS Queue
DS Queue
Types of Queues
Array Representation
Linked List Representation
Circular Queue
Deque
Priority Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Bubble Sort
Bucket Sort
Comb Sort
Counting Sort
Heap Sort
Insertion Sort
Merge Sort
Quick Sort
Radix Sort
Selection Sort
Shell Sort
Bitonic Sort
Cocktail Sort
Cycle Sort
Tim Sort
Differences
Linear vs non-linear
Array vs linked list
Stack vs queue
Linear vs Circular Queue
Linear Search vs Binary Search
Singly Linked List vs Doubly Linked List
Binary vs Binary Search Tree
Tree vs Graph
Binary Search tree vs AVL tree
Red Black Tree vs AVL tree
B tree vs B+ tree
Quick Sort vs Merge Sort
BFS vs DFS
Stack vs Heap
Bubble sort vs. Selection sort
Stack vs Array
Full Binary Tree vs Complete Binary Tree
Binary Tree vs B Tree
Primitive vs non-primitive data structure
Data types vs data structure
Misc
Trie Data Structure
Heap Data Structure
Splay Tree
Fundamental of the DS
Hash Table
Preorder Traversal
Tree Traversal
Implementation of Queue using Stacks
Implementation of Stack using Queue
Binomial Heap
Postorder Traversal
Sparse Matrix
Detect loop in a Linked list
Inorder Traversal
Convert Infix to Postfix notation
Convert infix to prefix notation
Conversion of Prefix to Postfix expression
Conversion of Postfix to Prefix expression
Remove the loop in a Linked List
Implement two stacks in an array
Reverse a stack using recursion
Detect cycle in a directed graph
Optimal Binary Search Tree
Priority Queue using Linked list
Balanced Binary Search Tree
Boundary Traversal of Binary tree
Diagonal Traversal of Binary Tree
Vertical Traversal of a Binary tree
Graph Algorithms
Time Complexity of Sorting Algorithms
Applications of Stack in Data Structure
Dictionary Data Structure
Structured Data and Unstructured Data
List Data Structure
Types of Tree in Data Structure
Abstract data type in data structure
Disjoint set data structure
Dynamic Data Structure
Hash Function in Data Structure
Complete Binary Tree
Threaded Binary Tree
Diameter of Binary Tree
Height of Binary Tree
Inorder Tree Traversal without Stack
Enumeration of Binary Trees
Maximum Width of a Binary Tree
Types of Graph in Data Structure
Primitive Data Type
Semi-Structured Data
Advance Data Structures
Sort an Array of 0's, 1's, and 2's
Stock Span Problem
Implementation of Deque by Circular Array
Rotate Operation in Linked List
Subarray with given sum
Self-organizing List
Unrolled Linked List
Types of Sparse Matrices
Application of Linked List
Topological Sorting
Ternary Search Tree
Stock Span Problem
Treap Data Structure
Quicksort on Doubly Linked List
Inversion count
Expression tree in DS
Garbage Collection in DS
Merge Sort on Doubly Linked List
Sort Stack using Recursion
LIFO Approach in data structure
Big O Notation in DS
Binary Tree Traversal in DS
Queue Operations in DS
What is a Non-Linear Data Structure
FIFO Approach in data structure
What are connected graphs in data structure
Which Python data structure is immutable
Which data structure is used by map
What is iteration in data structure
What are linear search and binary search in data structure
Hash Table vs STL Map
Recaman's Sequence
Maximum area rectangle created by selecting four sides from an array
Maximum number of distinct nodes in a root-to-leaf path
Hashing - Open Addressing for Collision Handling
Introduction to Hashing
Separate chaining for Collision Handling
Check if a given array contains duplicate elements within k distance from each other
Given an array A[] and a number x, check for pair in A[] with sum as x (aka Two Sum)
Find number of Employees Under every Manager
Union and Intersection of two Linked Lists
Kth Largest element in an array
Sort an almost-sorted, k-sorted or nearly-sorted array
Fibonacci Heap
Find whether an array is subset of another array
Print a Binary Tree in Vertical Order
Tournament Tree (Winner Tree)
Lazy Propagation in Segment Tree
Segment Tree - Range Minimum Query
Segment Tree - Sum of given Range
2-3 Trees (Search, Insertion, and Deletion)
Print kth least significant bit of a number
Add two numbers represented by linked lists
Adding one to the number represented as array of digits
Find precedence characters form a given sorted dictionary
Check if any anagram of a string is palindrome or not
Minimum Insertions to form a Palindrome
Allocate Minimum Number of Pages
Assembly Line Scheduling
Breadth First Search or BFS for a Graph
Find an element in array such that sum of the left array is equal to the sum of the right array
Bridges in a Graph
Bubble Sort in JavaScript
Burn the Binary tree from the Target node
Lowest Common Ancestor in a Binary Search Tree
Types of Hash Functions in C
Implement Dynamic Deque using Templates Class and a Circular Array
Iterative Depth First Traversal of Graph
Linked List Data Structure in C++ With Illustration
Reverse a Linked List in Groups of Given Size
Reverse Alternate K nodes in a Singly Linked List
When should I use a List vs a LinkedList
Why is deleting in a Singly Linked List O(1)
Construct Full Binary Tree using its Preorder Traversal and Preorder Traversal of its Mirror Tree
Find Relative Complement of two Sorted Arrays
Handshaking Lemma and Interesting Tree Properties -DSA
How to Efficiently Implement kStacks in a Single Array
Write C Functions that Modify Head Pointer of a Linked List
Introduction to Ant Colony Optimization
What is Array
The practical Byzantine Fault Tolerance (pBFT)
Applications of Queue Data Structure
Line Graph
Symmetric Binary Tree
AVL Tree Advantages
AVL Tree Time Complexity
Merge Two Binary Trees
Stack Operations in Data Structure
Self-Balancing Binary Search Trees
Sliding Window Maximum (Maximum of all Subarrays of size K)
AVL Trees Operations
Limitations of Stack in Data Structures
Representation of stack in data structure
Advantages of Threaded Binary Tree
Serialize and Deserialize a Binary Tree
Application of Binary Tree
AVL Tree Applications
B Tree Visualization
Properties of AVL Trees
Push and Pop Operation in Stack in Data Structure
Binary Search Tree Implementation
Find Maximum Sum by Replacing the Subarray in Given Range
Find The Number N, Where (N+X) Divisible By Y And (N-Y) Divisible By X
Find Values of P and Q Satisfying the Equation N = P^2.Q
What is the Balance Factor of AVL Tree
AVL Tree Implementation in Golang
Concatenation of two Linked Lists in O(1) time
Find Minimum Area of Rectangle Formed from Given Shuffled Coordinates
Find the Length of Maximum Path in Given Matrix for Each Index
How to Parse an Array of Objects in C++ Using RapidJson
Largest BST in Binary Tree
How to Print String Literal and Qstring With Qdebug in C++
Properties of Binary Tree
Right View of Binary Tree
Strict Binary Tree
Difference between Comb Sort and Shell Sort
Full Binary Tree
Left View of a Binary Tree
Level order Traversal in a Binary Tree
Lowest Common Ancestor of a Binary Tree
Top View of a Binary Tree
Types of Binary Trees
B Tree Insertion
Evaluation of a Postfix notation
B+ Tree Insertion
Bottom View of a Binary Tree
AVL Tree Program in C
B Tree Applications
B Tree Properties
How to Search, Insert, and Delete in an Unsorted Array
Count Non-Leaf Nodes in a Binary Tree
Get the Level of a Given Key in a Binary Tree
Double Ended Priority Queue
B+ Tree Deletion
B+ Tree Insertion
Checking for the Mirror Images in the Binary Trees
Count Non-Leaf Nodes in a Binary Tree
Get a Parent Binary Tree
Get All Descendants of the Binary Tree Element
Get the Level of a Given Key in a Binary Tree
Flatten Binary Tree to Linked List
Formula to Find a Level of the Node in a Binary Tree
Substring with Maximum Number of Vowels of Given Length (k)
Flatten Binary Tree to Sorted Linked List
Floor and Ceiling in Binary Search Tree
Find Level in a Binary Tree with Max Sum
Find kth Smallest Element in a Binary Search Tree
Find Next Greater Element in Binary Tree
Hashing in Data Structure
Primitive Data Structure
Find if Binary Tree Satisfies Balanced Height Property
Find the Largest Perfect Binary Tree in a Given Tree
Find Immediate Parents of Two Nodes in a Binary Tree
Applications, Advantages and Disadvantages of Circular Doubly linked List
Sorting Techniques in Data Structures
Find Clockwise Array in Binary Search Tree
Find Duplicate Subtrees in Binary Tree
Find the Index of the Number Using a Binary Tree
Find the In-Order Successor of a Node in a Binary Tree
Reversing a Queue
Different Types of Stack Operations
Time Complexity in Data Structure
Arrays are best Data Structure
Dynamic memory allocation in Data Structure
Application of Data Structure
Applications of Tree in Data Structure
How to Check if a Binary Number is Divisible by 3
Stock Buy and Sell Problem
Find Minimum in Rotated Sorted Array
Interpolation Search vs. Binary Search
Boggle (find all possible words in a board of characters)
Difference Between Prim's and Kruskal's algorithm
Interpolation Search
Quick Sort Using Hoare's Partition
Longest common substring
Longest Repeated Substring
Substring Check
Clone a Binary Tree with Random Pointers
How to efficiently implement k stacks in a single array
Kasai's algorithm for construction of LCP array from Suffix array
Strassen's Matrix Multiplication
suffix array introduction
Suffix Array nLogn Algorithm
Suffix tree introduction
Binary indexed tree
Given a n x n square matrix, find the sum of all sub-squares of size k x k
Inplace MxN size matrix transpose
longest palindrome substring
Maximum Size Square Sub-matrix with all 1s
Maximum Sum Rectangle in a 2D Matrix
Printing All Elements in Sorted Order from Row and Column Wise Sorted Matrix
Arraylist vs linked list
Diameter of an N-ary Tree
Generic Trees (N-ary Trees)
Level Order Traversal of N-ary Tree
Mirror of n-ary Tree
Serialize and Deserialize an N-ary Tree
Sum of all elements of N-ary Tree
The Great Tree-List Recursion Problem
Two dimensional Binary Indexed Tree or Fenwick Tree
Binary Indexed Tree Range Updates and Point Queries
Binary Indexed Tree Range Updates and Range Queries
Closest greater or same value on left side for every element in array
Construct an array from its pair-sum array
Equilibrium index of an array
Fermat's Factorization Method in Java
Find a triplet that sum to a given value in an array
Find k numbers with most occurrences in the given array
Find maximum value of Sum(i*arr[i]) with only rotations on given array allowed
Handshaking Lemma and Interesting Tree Properties
Implementation of Dynamic Segment Trees with Poly Hash Tables
Majority Element
Maximum equilibrium sum in an array
Maximum profit by buying and selling a share at most twice
Median in a stream of integers (running integers)
Merge Sort Tree for Range Order Statistics
Merge two sorted arrays with O(1) extra space
Minimum increment by k operations to make all elements equal
Minimum number of jumps to reach end
MO's Algorithm
Search in a row-wise and column-wise sorted matrix
Smallest subarray with sum greater than a given value
Sparse Table
Square Root (Sqrt) Decomposition Algorithm
Two Pointers Technique
Compressed segment trees and merging sets in O(N*logN)
Intersection of Linked List
Intersection Point in Y shaped linked list
Make Array Zero By Subtracting Equal Amounts In Java
Maximum Sum Pair with Equal Highest Digits
Minimum Possible value of |ai + aj - k| for given array and k
Tango Tree Data Structure
Check if two arrays are equal or not
Construct BST from its given level order traversal
Elements to be added so that all elements of a range are present in the array
Find Missing Elements in Range
K-th Largest Sum Contiguous Subarray
Minimum number of subsets with distinct elements
Minimum product of k integers in an array of positive integers
The non-overlapping sum of two sets
Palindrome substring queries
Recaman's Sequence
The sum of Elements Between k1th and k2th smallest elements
Print Matrix in a Snake Pattern
An Interesting Method to Generate Binary Numbers from 1 to n
Bottom View of a Binary Tree
Circular List Application
Deleting a Node in a Linked List
Diameter of a Binary Tree
Find distance between two nodes of a Binary Search Tree
Inorder Tree Traversal without Recursion
Inorder Tree Traversal without recursion and stack!
Maximum product of indexes of next greater on left and right
Print Left View of a Binary Tree
Remove all leaf nodes from the binary search tree
Sort a stack using a temporary stack
Split a Circular List into 2 Halves
Check given array of size n can represent BST of n levels or not
Construct a linked list from 2D matrix
In place, convert BST into a Min-Heap
Polish and Reverse Polish Notation
Suffix Trees in data structure
Weight Balanced Binary Tree
Transform a BST to greater sum tree
Vertical order traversal of Binary Tree using Map
Application of heap tree
Construct a linked list from 2D matrix
Define Abstract Data Type in Data Structure
Detect and Remove Loop in a Linked List
Difference Between a Tree and a Forest in Data Structures
Difference between bubble sort and merge sort
Difference between merge sort and quick sort
Explain double ended queue in detail
Find the median from running data stream
Flattening a Linked List
Generate All Subarrays
Heap memory vs. stack memory
Huffman encoding
Huffman Tree in Data Structure
Implementation of Graph in JavaScript
K-D Tree in Data Structures
Knapsack Problem in Data Structure
Largest Sum Contiguous Subarray (Kadane's Algorithm)
Multiway Trees in Data Structures
Optimal binary search tree in data structure
polynomial addition in data structure
Postfix deferred queue
Properties of tree in data structure
Recurrence Relation of Merge Sort
Recursive Bubble Sort
RSS linked list
Search in a Rotated Sorted Array
Sort an array of 0s, 1s and 2s | Dutch National Flag problem
Assign directions to edges so that the directed graph remains acyclic
Dependency Graph
Diameter of an N-ary tree
Height of n-ary tree if parent array is given
Introduction to Heavy Light Decomposition
LCA in a binary tree using RMQ
Number of Siblings of a given node in n-arr tree
Number of ways to traverse an N-arr
XOR Linked List - A Memory Efficient Doubly Linked List
Callback Queue
Inorder Predecessor and Successor in a Binary Search Tree
What is Internal Sorting
Block Swap Algorithm for Array Rotation in Python
CHECK FOR BALANCED BRACKETS IN AN EXPRESSION (WELL FORMEDNESS)
Count pairs from two BSTs whose sum is equal to given value x
Counting Inversions Problem in Data Structure
Differences between Insertion Sort and Selection Sort
LEFTIST TREE / LEFTIST HEAP
Find if there is a triplet in a balanced bst that adds to zero
Find the Maximum English Letter Present in Both Lowercase and Uppercase
K-way Merge Sort
Perfect Binary Trees
Reverse Sort
Scapegoat Trees
Stack Organisation
Time Complexity of using heap
Two-way merge sort
Validity of a given Tic-Tac-Toe board configuration
Weighted Prefix Search
Binary Tree to CDLL
Check if a Binary Tree is a Subtree of Another Binary Tree
Check if the Given String of Words can be Formed from Words Present in the Dictionary
Count sort vs bucket sort
FIFO vs LIFO approach in Programming
If you are given two traversal sequences, can you construct the binary tree
Linked List Deletion (Deleting a key at a given position)
Mastering Bracket Problems for Competitive Programming
Merge Overlapping Intervals
MIRROR OF MATRIX ACROSS DIAGONAL
Pair of strings having longest common prefix of maximum length in given array
Print all Possible Combinations of Words from the Dictionary using Trie
Segment Tree (Range Maximum Query with Node Update)
Tree Vertex Splitting in data structure
Why is Binary Heap Preferred over BST for Priority Queue
Arrange Consonants and Vowels in a linked list
Copy a linked list with next and arbit pointer
Kahn's Algorithm vs DFS Approach: A Comparative Analysis
Minimum flip required to make Binary Matrix symmetric
Sorted insert for circular linked list
C++ Program for Arranging Single Linked List in Alternate Odd and Even Nodes Order
Reservoir sampling in C++
0/1 Knapsack using Least Cost Branch and Bound
Merge K Sorted Linked Lists using Min Heap
Number of elements greater than K in the range L to R using Fenwick Tree (Offline queries)
Detect Cycle in Graph using DSU
Merkle Tree and Hash Chain Data Structures with a difference
Create a matrix with alternating rectangles of O and X
Find the first non-repeating character from a stream of characters
Find the first circular tour that visits all petrol pumps
Find the tasks completed by soldiers based on their ranks
K-th Largest Sum Contiguous Subarray
Numbsubarrayer of elements less than or equal to a given number in a given
Queries to add, remove and return the difference of maximum and minimum
Time Complexity of building a heap
Build linear type suffix
Count of Valid Splits in a String
Delete all occurrences of a given key in a linked list
Design a data structure that supports insert, delete, search and getRandom in constant time
Find the largest subarray with 0 sum
Free Tree in Data Structures
How to insert Strings into an AVL Tree
Longest Consecutive Subsequence
Merge two binary Max Heaps
Secure Message Encoding
Sort an almost sorted array
Tree of Space - Locking and Unlocking N-Ary Tree
Triply Linked list
COUNT OF ZEROES
Design a Chess Game
Design a data structure that supports insert, delete, search and getRandom in constant time
Design and Implement Special Stack Data Structure
Enhancing Password Strength
Enumeration of Binary Tree
Eulerian and Hamiltonian path
Fair Array Removal Indices
Find the Absolute Difference between the Right View Sum of two Binary Trees
Find the number of colored nodes according to given queries in a full Binary Tree
Finding Minimum Steps in Special Binary Tree
Finding the Largest Multiple of Three
Flatten a binary tree into linked list
General Tree (Each node can have arbitrary number of children) Level Order Traversal
Generating the Maximum Number from Two Arrays
Hashing and its Applications
Islands in a graph using BFS
Iterative Letter Combinations of a Phone Number
K-way Merge Sort
Maximize Total Score
PERMUTED ROWS IN A MATRIX
Remove extra edge from a BST
Van Emde Boas Tree
Which Minimum Spanning Tree Algorithm is better
Ackermann Function
BINARY TO SYMMETRIX
INPLACE MATRIX TRANSPOSE
Print all words matching a pattern in CamelCase Notation Dictionary
Reduce the string by removing K consecutive identical characters
Subtraction in Linked List
TRANSITIONS OF MATRIX
Blending vs Stacking
Bloom Filters
Count Array Pairs Divisible by k
Counting Beautiful Numbers in a Specified Range
Find the Closest Palindrome
Minimizing water collection distance in javaT village
Minimum Array Length After Pair Removals
Nth even Fibonacci Sequence
Persistent Data Structure
Queue for Competitive Programming
Recursively remove all adjacent duplicates
Remove the letter to equalize the frequency
Chocolate Distribution Problem
Find out the person who got the ticket last problem in queue
Product Array Puzzle
MCQs on backtracking
Design a data structure that supports insert, delete, search, and getRandom in constant time
Assign directions to edges so that the directed graph remains acyclic
Print the frequency of each character in Alphabetical order
Check if a queue can be sorted into another queue using a stack
Auto-complete feature using Trie
Connect nodes at same level
Construct Tree from Given Inorder and Preorder Traversals
Decimal Equivalent of Binary Linked List
How do you implement Stack using Priority Queue or Heap
Introduction to Monotonic Stacks
Minimum Initial Points to Reach Destination
Print Ancestors of a given node in Binary Tree
Priority Queue using Doubly Linked List
Shortest distance between two cells in a matrix or grid
Sort an Array in Wave Form
Burn the binary tree starting from the target node
Check for possible paths in the 2D Matrix
Find Triplets with zero-sum
Print a Given Matrix in Spiral form
Alien Dictionary problem in dsa
Array Pair Sum Divisibility Problem
DIFFERENCE BETWEEN GREEDY AND DIVIDE AND CONQUER
How do you check if a given array represents a heap
LINKED LIST REVERSE
MAXIMUM SIZE RECTANGLE
Priority queue of pairs in C++ with ordering by first and second element
Reversing Individual Words and Unveiling the Secrets of Histograms
Sliding SubArray Beauty
Two Pointer Technique
UGLY NUMBERS IN DSA
Check for Balanced Brackets in an expression
Largest Number After Digit Swaps By Parity
Minimize Deviation In Array
Print a given matrix in spiral form
Print unique rows in a given Boolean matrix
Restrictive Candy Crush
Search in a row wise and column wise sorted matrix
SIP Stack
Stacked Bar Chart
Search Query Auto Complete
Applications of the greedy algorithm
Applications, Advantages and Disadvantages of Arrays
Applications, Advantages and Disadvantages of Queue
Applications, Advantages and Disadvantages of Stacks
Floor and Ceil from a BST
India Stack
Next Higher Palindromic Numbers using the Same Set of Digits
QuickSort on Singly Linked List
Reverse a Number using Stacks
Serialize and Deserialize an N-ary Tree
Stack Pointer
What is a K-connected Graph
Append K Integers with Minimal Sum Problem
Circular Linked Lists Introduction and Application
Detect cycle in an undirected graph in C++
Detect Cycle in Graph using DSU
Find the maximum number of marked indices problem
Generalized Suffix Tree
Interval Tree
Maximum Number of Tasks Assignment Problem
Merge K Sorted Lists
Triplet sum closest to given number
Apply Operations To Maximize Frequency Score
Difference between malloc and realloc
Merge Sort on Singly Linked Lists
Minimum Number Of Frogs Croaking
Total Distance Travelled
X Of A Kind In A Deck Of Cards
Applications, Advantages and Disadvantages of Linked List
Balls rolling in the maze
Destroy Sequential Targets
Difference Between Push and Pop in Stack
Dynamic Programming (DP) on Grids
Find all good strings problem in Data Structure
Find Itinerary from a given list of tickets
Height of n-ary tree if parent array is given
Maximum Deletions on a String
Reversal algorithm for Array rotation
Reverse Pairs Problem in Data Structure
String Hashing using the Polynomial Rolling Hash Function
The Great Tree-List Recursion Problem
Trapping of rainwater problem in Data Structure
What Does Big O(N^2) Complexity Mean
How to handle duplicates in Binary Search Tree
Optimal cell in matrix to collect maximum coins
Maximizing Chocolates in Grid using 2 robots
Create a matrix with alternating rectangles of O and X
Interleave the first half of the queue with the second half
The sum of all elements between k1'th and k2'th smallest elements
Binary Indexed Tree Range Updates and Point Queries
Burn the binary tree starting from the target node
Check Matrix Transformation by Flipping Sub-Matrices along the Principal or Anti-Diagonal
DFS for an n-ary Tree(Acyclic Graph) Represented as an Adjacency List
Difference Between Counting Sort and Bucket Sort
Internal Data Structures and Time Complexity Table of All the C++ STL Containers
K Centres Problem (Greedy Approximate Algorithm)
Left Rotation and Right Rotation of a String
Merge Two Sorted Linked Lists
Move all Zeroes to End of Array
Number of flips to make binary string alternate
Program to Reveal the Positions in Minesweeper
Tarjan's Algorithm to Find Strongly Connected Components
Difference between big o and big theta ? and big omega ? notations
DS MCQ
Count Array Pairs Divisible by kProblem statementGiven a 0-indexed integer array nums of length n and an integer k, return the number of pairs (i, j) such that:
Java Approach 1 Frequency CountingOutput: 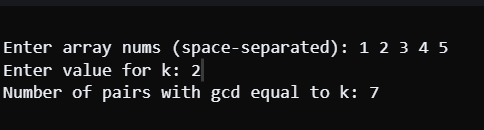
Code Explanation:
Time complexity:
Space complexity:
Drawbacks:
Java Approach 2 Using Combination of Counting and CombinatoricsOutput: 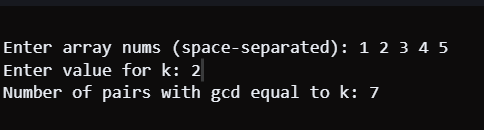
Code explanation:
Time complexity:
Space complexity:
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









