Insertion Sort Algorithm

In this article, we will discuss the Insertion sort Algorithm. The working procedure of insertion sort is also simple. This article will be very helpful and interesting to students as they might face insertion sort as a question in their examinations. So, it is important to discuss the topic.

Insertion sort works similar to the sorting of playing cards in hands. It is assumed that the first card is already sorted in the card game, and then we select an unsorted card. If the selected unsorted card is greater than the first card, it will be placed at the right side; otherwise, it will be placed at the left side. Similarly, all unsorted cards are taken and put in their exact place.

The same approach is applied in insertion sort. The idea behind the insertion sort is that first take one element, iterate it through the sorted array. Although it is simple to use, it is not appropriate for large data sets as the time complexity of insertion sort in the average case and worst case is O(n²), where n is the number of items. Insertion sort is less efficient than the other sorting algorithms like heap sort, quick sort, merge sort, etc.

Insertion sort has various advantages such as -

• Simple implementation
• Efficient for small data sets
• Adaptive, i.e., it is appropriate for data sets that are already substantially sorted.

Now, let's see the algorithm of insertion sort.

Algorithm

The simple steps of achieving the insertion sort are listed as follows -

Step 1 - If the element is the first element, assume that it is already sorted. Return 1.

Step2 - Pick the next element, and store it separately in a key.

Step3 - Now, compare the key with all elements in the sorted array.

Step 4 - If the element in the sorted array is smaller than the current element, then move to the next element. Else, shift greater elements in the array towards the right.

Step 5 - Insert the value.

Step 6 - Repeat until the array is sorted.

Working of Insertion sort Algorithm

Now, let's see the working of the insertion sort Algorithm.

To understand the working of the insertion sort algorithm, let's take an unsorted array. It will be easier to understand the insertion sort via an example.

Let the elements of array are -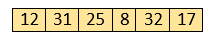

Initially, the first two elements are compared in insertion sort.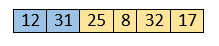

Here, 31 is greater than 12. That means both elements are already in ascending order. So, for now, 12 is stored in a sorted sub-array.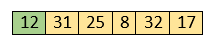

Now, move to the next two elements and compare them.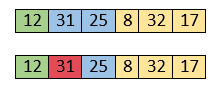

Here, 25 is smaller than 31. So, 31 is not at correct position. Now, swap 31 with 25. Along with swapping, insertion sort will also check it with all elements in the sorted array.

For now, the sorted array has only one element, i.e. 12. So, 25 is greater than 12. Hence, the sorted array remains sorted after swapping.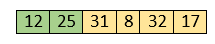

Now, two elements in the sorted array are 12 and 25. Move forward to the next elements that are 31 and 8.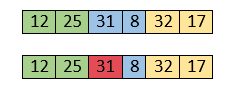

Both 31 and 8 are not sorted. So, swap them.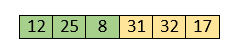

After swapping, elements 25 and 8 are unsorted.

So, swap them.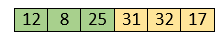

Now, elements 12 and 8 are unsorted.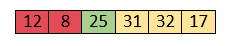

So, swap them too.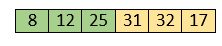

Now, the sorted array has three items that are 8, 12 and 25. Move to the next items that are 31 and 32.

Hence, they are already sorted. Now, the sorted array includes 8, 12, 25 and 31.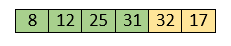

Move to the next elements that are 32 and 17.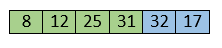

17 is smaller than 32. So, swap them.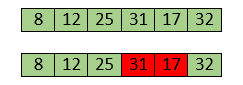

Swapping makes 31 and 17 unsorted. So, swap them too.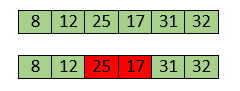

Now, swapping makes 25 and 17 unsorted. So, perform swapping again.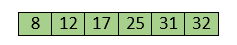

Now, the array is completely sorted.

Insertion sort complexity

Now, let's see the time complexity of insertion sort in best case, average case, and in worst case. We will also see the space complexity of insertion sort.

1. Time Complexity

• Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of insertion sort is O(n).
• Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of insertion sort is O(n²).
• Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of insertion sort is O(n²).

2. Space Complexity

• The space complexity of insertion sort is O(1). It is because, in insertion sort, an extra variable is required for swapping.

Implementation of insertion sort

Now, let's see the programs of insertion sort in different programming languages.

Program: Write a program to implement insertion sort in C language.

Output:

Program: Write a program to implement insertion sort in python.

Output: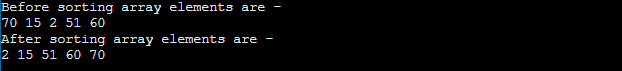

Program: Write a program to implement insertion sort in C++ language.

Output:

Program: Write a program to implement insertion sort in C# language.

Output:

Program: Write a program to implement insertion sort in Java.

Output:

Program: Write a program to implement insertion sort in PHP.

Output:

So, that's all about the article. Hope the article will be helpful and informative to you.

This article was not only limited to the algorithm. We have also discussed the algorithm's complexity, working, and implementation in different programming languages.