DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Inplace MxN size matrix transposeMatrix transposition is a fundamental operation in linear algebra that involves swapping rows and columns of a matrix. In this Article, we will explore the concept of in-place matrix transposition for matrices of size m x n, and provide a detailed explanation along with Java code to implement this operation. Understanding In-Place Matrix Transposition Matrix transposition involves interchanging rows and columns of a matrix. For an m x n matrix, the transposed matrix will have dimensions n x m. In the context of in-place transposition, we aim to achieve this transposition without using additional memory space for a new matrix. Instead, we will manipulate the existing matrix elements to achieve the transposed form. Algorithm for In-Place Matrix Transposition The algorithm for in-place matrix transposition can be summarized in the following steps:
By following this algorithm, we ensure that each element is swapped with its corresponding element across the main diagonal of the matrix. Here's a step-by-step breakdown of the Java code implementing the in-place matrix transposition algorithm: Output: 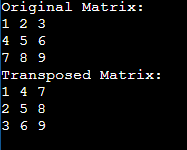
Step by step Explanation of the above code:
Time Complexity of the entire code: O(n^2 + m * n) Let's brake down the time complexity for better understanding
Thus, the time complexity of the transpose method is O(n^2+ m * n), where n is the number of columns and m is the number of rows. Space Complexity of the entire code: O(1) Since we are not making use of any additional space in order to transpose the matrix since it space complexity would be O(1).
Next Topiclongest palindrome substring
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









