Inorder Predecessor and Successor in a Binary Search Tree

Binary search trees (BSTs) are a famous data structure that stores data in a way that allows quick lookups, insertions, and deletions. An important concept when working with BSTs is finding the in-order predecessor and successor of a node. The inorder predecessor of a node is the node that would come immediately before it in an inorder traversal of the BST. Similarly, the inorder successor is the node that would go directly after. Being able to find these nodes quickly is helpful for many BST operations. In this article, we'll look at how to find in-order predecessors and successors in a binary search tree.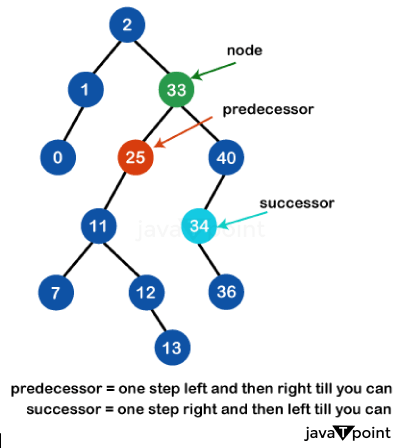

Inorder Traversal Refresher

Before jumping into predecessors and successors, let's do a quick review of inorder traversal. Inorder traversal of a BST visits the nodes in ascending order. It works by recursively traversing the left subtree, calling the current node, and then recursively traversing the right subtree. For example, here is how inorder traversal would work on the following sample BST:

The nodes would be visited in the order of 2, 5, 8, 15, 17, 20, and 25.

So when we talk about a node's inorder predecessor or successor, we mean the node that comes immediately before or after it in this inorder sequence.

Finding Inorder Predecessor

Let's start with finding a node's inorder predecessor. The inorder predecessor is the node that would come immediately before the node during an inorder traversal.

There are a few critical cases to consider here:

Node has left subtree

If the node has a non-empty left subtree, then the predecessor is the rightmost node in that subtree. We can find it by starting at the node's left child and repeatedly following right child pointers until we can't anymore.

For example, the predecessor of 15 in the example tree would be 8. We start at 15's left child 5, then go right once to 8.

The node is the left child of the parent.

If the node is the left child of its parent, then the parent is the predecessor.

So, for node 5, its predecessor would be 2 (its parent).

Node is the right child of a parent.

If the node is the right child of its parent, then we need to recursively go up the tree following left child pointers until we find a node that is the left child of its parent. That parent is the predecessor.

The predecessor of 17 is 15 because 17 is the right child. So we go up to 20 and follow its left child pointer to 15.

Node has no left subtree and is not a left child.

In this case, we recursively keep going up the tree following parent pointers until we find a node that meets one of the previous cases.

The predecessor of 25 is 20 since 25 has no left subtree and is not a left child. We traverse until we find 20, which is the left child of its parent.

So, in summary, to find the inorder predecessor:

1. If the node has a left subtree, return the rightmost node in the left subtree
2. If the node is left child of the parent, return parent
3. Else, keep traversing up recursively until you find a node that meets #1 or #2

Finding Inorder Successor

The inorder successor can be found using similar logic but reversing left and right.

The successor is the node that comes immediately after the node during an inorder traversal.

The critical cases are:

Node has the right subtree

If the node has a non-empty right subtree, then the successor is the leftmost node in that subtree.

For 8, its successor would be 15, since 15 is the leftmost node in 8's right subtree.

Node is the right child of a parent.

If the node is the right child of its parent, then the parent is the successor.

So the successor of 20 is 25.

The node is the left child of the parent.

If the node is the left child of its parent, then we traverse up recursively, looking for a node that is the right child of its parent. That parent is the successor.

17's successor is 20 since 17 is a left child. We go up to 15 and follow its right child pointer to 20.

Node has no right subtree and is not a right child

In this case, we keep traversing until we find a node that satisfies one of the other cases.

5's successor is 8 since it has no right subtree and is not a right child. We traverse up to 15 and then follow its right child to 8.

In summary, to find the inorder successor:

1. If the node has a right subtree, return the leftmost node in the right subtree
2. If the node is the right child of the parent, the return parent
3. Else, keep traversing up recursively until you find a node that meets #1 or #2

Python Implementation

Approach 1: Recursive Approach

Here is an introduction to the recursive approach for finding order predecessor and successor in a binary search tree:

In a binary search tree (BST), the nodes are arranged such that the left subtree of a node contains values less than the node, and the right subtree contains values greater than the node. This property allows us to search efficiently.

Another helpful property of BSTs is that an in-order traversal of the tree visits the nodes in sorted order. The node called before a given node is its inorder predecessor, and the node seen just after is the inorder successor.

We can leverage these properties to find the inorder predecessor and successor of a given key recursively. The key idea is to traverse the BST recursively, keeping track of potential predecessor and successor nodes.

When traversing left, a node becomes a potential predecessor. When going right, it becomes a possible successor. Once we reach the node with the matching key, we must look at its left and right subtrees. The maximum value in the left subtree is the predecessor and the minimum value in the right subtree is the successor.

This recursive approach elegantly utilizes the BST structure to find predecessor and successor without needing auxiliary storage. We don't need to maintain a visited set. The recursion naturally ensures we don't repeat work. This makes the solution simple and efficient.

The recursive calls act as an implicit stack to track the potential candidates. Returning up the call stack gives us the answer. This demonstrates the power of recursion for tree problems. Overall, the recursive approach is intuitive and optimal, leveraging the innate BST structure.

Program

Output:

Inorder Predecessor: 20
Inorder Successor: 40

Explanation:

1. TreeNode class is defined to represent nodes of the binary tree. It has val, left and right attributes.
2. Solution class contains the findPredecessorSuccessor method to find predecessor and successor of given key.
3. findPredecessorSuccessor initializes predecessor and successor to None.
4. It defines an inorderTraversal helper function to traverse tree in inorder fashion.
5. inorderTraversal recursively traverses left subtree.
6. When node with key is found, predecessor and successor are set:
   • If left child exists, it is predecessor
   • If right child exists, it is successor
7. Temp variables are used to traverse left and right subtrees to find max and min valued nodes.
8. After setting predecessor and successor, inorder traversal continues.
9. findPredecessorSuccessor calls inorderTraversal on root to start traversal.
10. Main code creates sample tree, calls findPredecessorSuccessor to find for key=30.
11. Predecessor and successor are printed if found, else None is printed.

Approach 2: Iterative Approach

The recursive approach is an elegant solution that utilizes the innate structure of a binary search tree to find the predecessor and successor for a given key. However, recursion has its drawbacks - it consumes stack space proportional to the height of the tree and involves function call overheads. For very skewed or deep trees, we could run into stack overflow errors.

An alternative is to adopt an iterative approach. The key idea here is to traverse the binary tree iteratively using a pointer instead of recursive calls. We avoid recursion altogether. The traversal logic is encapsulated in a while loop, which iterates through the tree nodes systematically.

To track the potential predecessor and successor, we maintain two reference variables, which get updated when we take left or right turns during traversal. The core is that the pointer tracks our current position, while the reference variables track the parent nodes from where we arrived at the current node.

Once the node with a matching key is found, the reference variables will point to the predecessor and successor, respectively, based on the relative value comparisons done during traversal. We only need to check the node's left and right subtrees to confirm the final values.

This iterative style traversal consumes only O(1) auxiliary space since no recursion stack is involved. It is more space-efficient and can handle skewed trees gracefully. The iterative logic may also be more straightforward to understand compared to recursion. Overall, it complements the elegance of the recursive approach by providing an efficient and robust solution.

Algorithm:

• Initialize predecessor and successor variables to None. These will store the result.
• Create a pointer variable (curr) to traverse the BST iteratively. Initialize it to root.
• Use a while loop on curr to traverse BST till we find the matching key node.
• Before entering the loop, check if the curr is None and handle it appropriately.
• Inside the loop, compare curr's value with the key. There are 3 cases:
  1. If curr's value equals the key, we have found the node. Check its left and right subtrees to update predecessor and successor variables, respectively. Break out of the loop.
  2. If the curr's value is less than key, update the predecessor to curr and move curr to its right child.
  3. If the curr's value exceeds the key, update the successor to curr and move it to its left child.
• Moving curr left and right iteratively, we recursively traverse the BST but avoid function call overheads.
• The predecessor and successor nodes essentially track the parent nodes from where we took a left or right turns to reach the key node.
• Once the loop ends, return the predecessor and successor variables, which now contain the result nodes.

Advantages:

• Avoids the recursion overhead of function calls and stack. More efficient.
• Iterative code is often simpler to understand.
• It can handle very deep and skewed trees without blowing up the stack.

Output:

Inorder Predecessor: 30
Inorder Successor: 40

Here are the key points about this iterative approach:

• We initialize pred and succ to None to store the result.
• A curr pointer is used to traverse the BST iteratively.
• The main while loop runs till we find the node with a matching key.
• If curr.val == key, we have found the node. We check its left and right subtrees to populate pred and succ, respectively, using the find_max and find_min helper functions.
• If curr.val < key, curr becomes the potential predecessor so we update pred and move curr right.
• Else curr.val > key, so curr is a potential successor. We updated succ and moved to curr left.
• Once the key is found and pred, succ set, we break from the loop and return.
• By using the curr pointer to traverse, we avoid recursion. The while loop iterates through BST.
• The pred and succ nodes track the ancestor nodes from where we took left or right turns.
• When the key is found, pred and succ contain the nodes from where we reached the key last.
• Checking the key's left and right subtrees completes the picture.