Binary tree vs Binary Search tree

First, we will understand the binary tree and binary search tree separately, and then we will look at the differences between a binary tree and a binary search tree.

What is a Binary tree?

A Binary tree is a non-linear data structure in which a node can have either 0, 1 or maximum 2 nodes. Each node in a binary tree is represented either as a parent node or a child node. There can be two children of the parent node, i.e., left child and right child.

There is only one way to reach from one node to its next node in a binary tree.

A node in a binary tree has three fields:

• Pointer to the left child: It stores the reference of the left-child node.
• Pointer to the right child: It stores the reference of the right-child node.
• Data element: The data element is the value of the data which is stored by the node.

The binary tree can be represented as: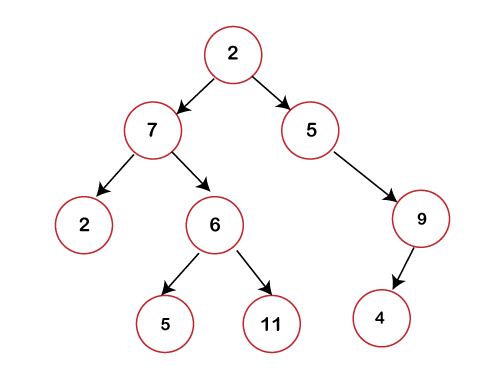

In the above figure, we can observe that each node contains utmost 2 children. If any node does not contain left or right child then the value of the pointer with respect to that child would be NULL.

Basic terminologies used in a Binary tree are:

• Root node: The root node is the first or the topmost node in a binary tree.
• Parent node: When a node is connected to another node through edges, then that node is known as a parent node. In a binary tree, parent node can have a maximum of 2 children.
• Child node: If a node has its predecessor, then that node is known as a child node.
• Leaf node: The node which does not contain any child known as a leaf node.
• Internal node: The node that has atleast 2 children known as an internal node.
• Depth of a node: The distance from the root node to the given node is known as a depth of a node. We provide labels to all the nodes like root node is labeled with 0 as it has no depth, children of the root nodes are labeled with 1, children of the root child are labeled with 2.
• Height: The longest distance from the root node to the leaf node is the height of the node.

In a binary tree, there is one tree known as a perfect binary tree. It is a tree in which all the internal nodes must contain two nodes, and all the leaf nodes must be at the same depth. In the case of a perfect binary tree, the total number of nodes exist in a binary tree can be calculated by using the following equation:

n = 2^m+1-1

where n is the number of nodes, m is the depth of a node.

What is a Binary Search tree?

A Binary search tree is a tree that follows some order to arrange the elements, whereas the binary tree does not follow any order. In a Binary search tree, the value of the left node must be smaller than the parent node, and the value of the right node must be greater than the parent node.

Let's understand the concept of a binary search tree through examples.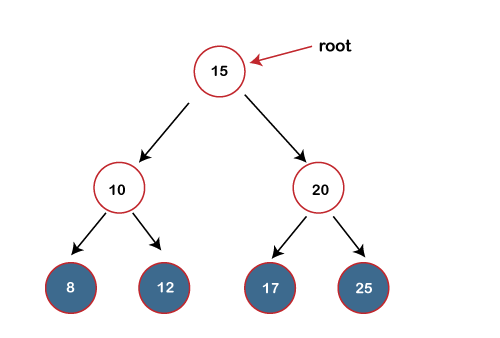

In the above figure, we can observe that the value of the root node is 15, which is greater than the value of all the nodes in the left subtree. The value of root node is less than the values of all the nodes in a right-subtree. Now, we move to the left-child of the root node. 10 is greater than 8 and lesser than 12; it also satisfies the property of the Binary search tree. Now, we move to the right-child of the root node; the value 20 is greater than 17 and lesser than 25; it also satisfies the property of binary search tree. Therefore, we can say that the tree shown above is the binary search tree.

Now, if we change the value of 12 to 16 in the above binary tree, we have to find whether it is still a binary search tree or not.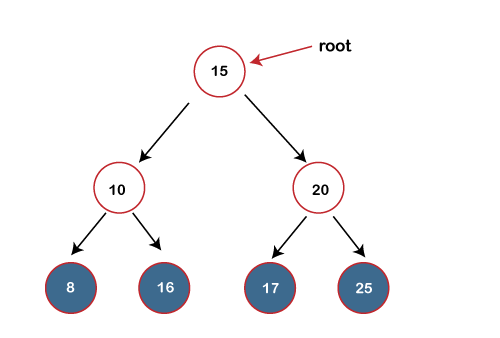

The value of the root node is 15 which is greater than 10 but lesser than 16, so it does not satisfy the property of the Binary search tree. Therefore, it is not a binary search tree.

Operations on Binary search tree

We can perform insert, delete and search operations on the binary search tree. Let's understand how a search is performed on a binary search. The binary tree is shown below on which we have to perform the search operation: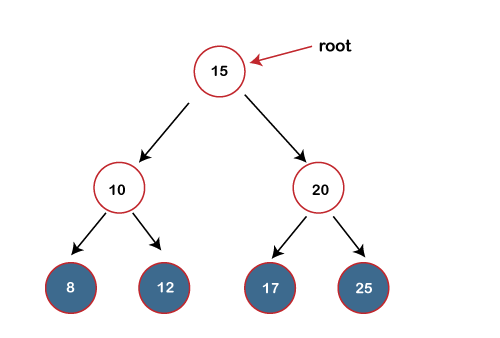

Suppose we have to search 10 in the above binary tree. To perform the binary search, we will consider all the integers in a sorted array. First, we create a complete list in a search space, and all the numbers will exist in the search space. The search space is marked by two pointers, i.e., start and end. The array of the above binary tree can be represented as

First, we will calculate the middle element and compare the middle element with the element, which is to be searched. The middle element is calculated by using n/2. The value of n is 7; therefore, the middle element is 15. The middle element is not equal to the searched element, i.e., 10.

Note: If the element is being searched is lesser than the mid element, then the searching will be performed in the left half; else, searching will be done on the right half. In the case of equality, the element is found.

As the element to be searched is lesser than the mid element, so searching will be performed on the left array. Now the search is reduced to half, as shown below:

The mid element in the left array is 10, which is equal to the searched element.

Time complexity

In a binary search, there are n elements. If the middle element is not equal to the searched element, then the search space is reduced to n/2, and we will keep on reducing the search space by n/2 until we found the element. In the whole reduction, if we move from n to n/2 to n/4 and so on, then it will take log₂n steps.

Differences between Binary tree and Binary search tree