DS Tutorial
DS Array
DS Linked List
DS Stack
DS Queue
DS Tree
DS Graph
DS Searching
DS Sorting
Differences
Misc
DS MCQ
Breadth First Search or BFS for a GraphWhat is a Graph?The graph is a data structure where we store the values in terms of nodes or vertices. Nodes are connected to each other via edges, where edges can be weighted or unweighted. If there is an edge between two nodes and it contains some weight then we call it a weighted graph. Otherwise, it is called an unweighted graph. An unweighted graph is a type of graph with no edge weight. In this type of graph, the edges represent the connection between two nodes. If there is an edge between nodes u and v in an unweighted graph then u and v are adjacent to each other. To traverse the graph, we use two approaches:
In DFS, we go to all the deepest nodes of the starting node using recursion. Here, we are talking about BFS. BFSBFS stands for breadth-first search, where we traverse all the neighboring nodes of the source node, and we solve it successively for the adjacent nodes. Traversal of nodes is done radially in BFS. For example: 
Next iteration- 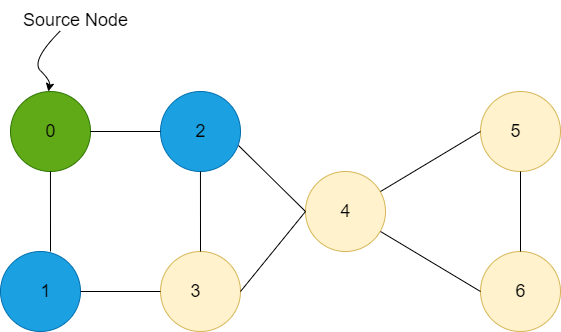
Next iteration- 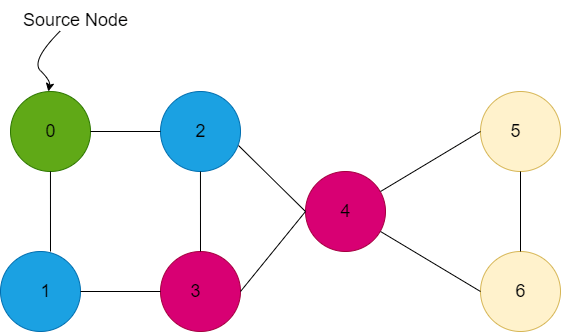
Next iteration- 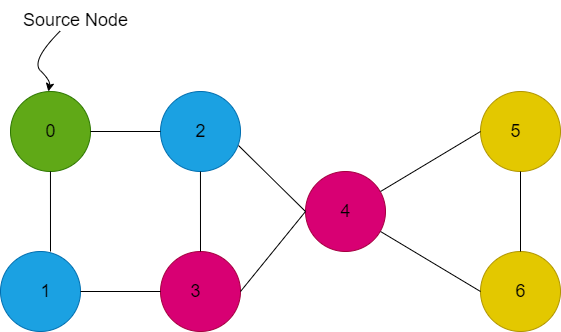
In the above example, the order of BFS will be: 0->1,2->3,4->5,6 We will use the queue data structure to get the BFS traversal of a graph. Java code:Output: 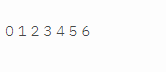
Explanation In the above example, we have a connected graph in the form of an adjacency list, where each node has the ArrayList of its neighbor nodes. Now to implement the BFS traversal, we use a queue data structure which is initially empty, and also we use a visited array of type Boolean to make sure we don't include that node which has already been covered in the breadth-first search traversal. Initially, we marked the source node as visited and added it into the queue. Now, we will iterate the loop until the queue becomes empty. At each time, we will remove the topmost element of the queue, add it to our answer and add its unvisited neighbor into the queue and mark them visited also. At first iteration- The queue has node 0 and we will add it into our answer, and its neighbor nodes 1 and 2 will be added into the queue and marked visited. Now q=1,2 and answer=0. Now we will remove one add into our answer, and its unvisited neighbor is 3. So now q=2,3 and answer =0,1 Now we will remove 2, add it to our answer and its unvisited neighbor is 4. So now q=3,4 and answer = 0,1,2 Now we will remove 3, add it to our answer and its unvisited neighbors are nothing. So now q=4 and answer = 0,1,2,3 Now we will remove 4, add it to our answer and its unvisited neighbors are 5,6. So now q=5,6 and answer = 0,1,2,3,4 Now we will remove 5, add it to our answer and its unvisited neighbor is nothing. So now q=6 and answer = 0,1,2,3,4,5 Now we will remove 6, add it to our answer and its unvisited neighbor is nothing. So now q=empty and answer = 0,1,2,3,4,5,6 Since the queue is empty, we will stop the loop and return from the functions, and we will print the result. Time complexity: O(N+E) where N is the number of nodes and E is the number of edges Space complexity: O(N) -> for visited array O(N) for result +O(N) for queue. If Graph is Not ConnectedIf the graph is not connected then we will have more than one source vertex for the graph. So we will call BFS for each component separately. For example: 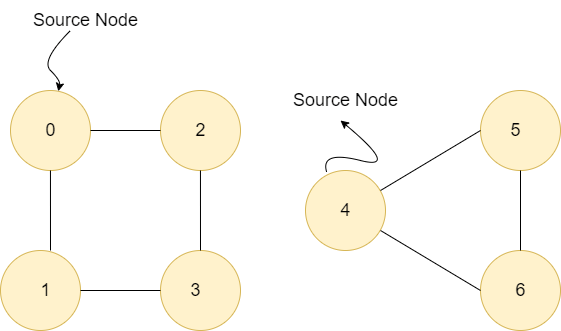
Java code: Output: 
Time complexity: O(N+E) where N is the number of nodes and E is the number of edges
Next TopicFind an element in array such that sum of the left array is equal to the sum of the right array
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









