Chocolate Distribution Problem

The "Chocolate Distribution Problem" (CDP) is a pleasant puzzle in computer science and algorithmic problem-solving. To effectively distribute chocolates among people with different taste preferences, this problem-which comes up frequently in interviews and competitive programming-requires the strategic application of data structures and algorithms. As we examine the complexities of this issue, we will comprehend the limitations, investigate its theoretical foundations, and dissect the algorithmic strategies that can be used to arrive at the best answer.

Problem Statement:

Consider a situation in which N people exist and each of them has a unique chocolate preference. The available chocolates are shown in an array, where each member indicates the chocolate's sweetness level. The objective is to divide up the M chocolates among the participants to reduce the variation in chocolate sweetness that any two participants may experience.

We can define the following to categorize the problem:

N: The total number of people
M: Amount of chocolates on hand
Chocolate array: A containing each chocolate's sweetness levels

Constraints:

1<=N<=10**9
1<=M<=N
0≤Sweetness level of chocolates≤10**9

Approach-1: Brute Force Method

The simplest method for solving the Chocolate Distribution Problem is to compute the difference in sweetness levels for any distribution that could exist. However, for larger inputs, this brute-force method is inefficient due to its O(N*M) time complexity. The following is the pseudocode for this method:

def cho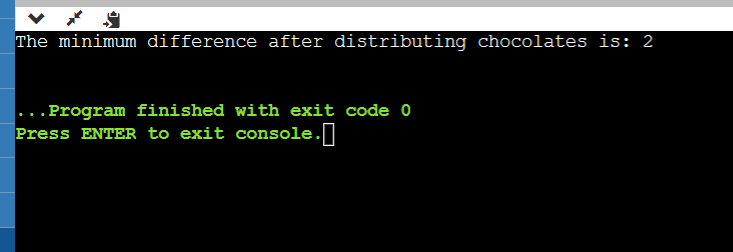colateDistribution(chocolates, N, M):
    chocolates.sort()  # Sort the chocolates array
    min_difference = float('inf')  # Initialize the minimum difference to positive infinity
    
    for i in range(N - M + 1):
        current_difference = chocolates[i + M - 1] - chocolates[i]
        min_difference = min(min_difference, current_difference)
    
    return min_difference

Output:

Although this method yields the right answer, it is not the best and cannot match the efficiency standards for big input sizes.

Approach-2: Sorting and Sliding Window

By distributing chocolates with comparable sweetness levels, we can minimize the difference and maximize the solution. By arranging the chocolate selection, we can examine neighboring components with comparable degrees of sweetness. We can quickly compute the minimum difference by using a sliding window of size M. Because of the sorting step, this technique has an O(N log N) time complexity.

def cho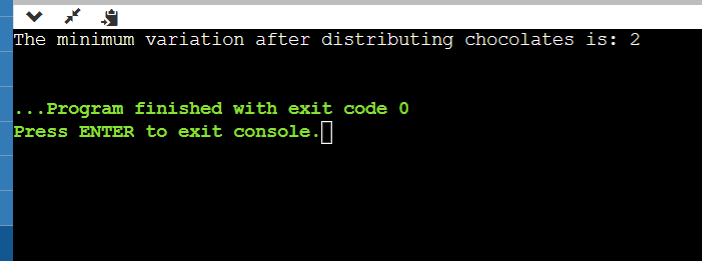colateDistribution(N, M, chocolates):
    chocolates.sort()  # Sort the chocolates array
    min_variation = float('inf')  # Initialize the minimum variation to positive infinity
    # Use a sliding window of size M to calculate the variation
    for i in range(N - M + 1):
        current_variation = chocolates[i + M - 1] - chocolates[i]
        min_variation = min(min_variation, current_variation)
    return min_variation

# Example input
N = 5
M = 3
chocolates = [3, 1, 4, 5, 2]

# Optimized solution using sorting and sliding window
result = chocolateDistribution(N, M, chocolates)

# Output
print(f"The minimum variation after distributing chocolates is: {result}")

Output:

Although this technique is more effective than the brute-force approach, there is still an opportunity for improvement, particularly about time complexity.

Approach 3: Optimal Solution with Time Complexity O(log N)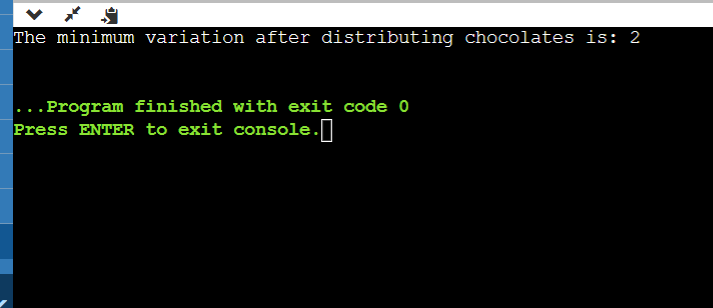

def chocolateDistributionOptimal(N, M, chocolates):
    chocolates.sort()  # Sort the chocolates array
    min_variation = float('inf')  # Initialize the minimum variation to positive infinity

    # Use two pointers to find the minimum variation
    left, right = 0, M - 1

    while right < N:
        current_variation = chocolates[right] - chocolates[left]
        min_variation = min(min_variation, current_variation)
        left += 1
        right += 1

    return min_variation

# Example input
N = 5
M = 3
chocolates = [3, 1, 4, 5, 2]

# Optimal solution using sorting and two-pointer approach
result = chocolateDistributionOptimal(N, M, chocolates)

# Output
print(f"The minimum variation after distributing chocolates is: {result}")

Output:

Beyond its theoretical significance, the Chocolate Distribution Problem finds practical applications in settings including load balancing and resource optimization.
Beyond its computational complexity, this topic is similar to real-world problems where minimizing workload disparity is crucial, including allocating jobs among servers or resources among teams.
The progression of optimized solutions from a brute-force method captures the iterative character of algorithmic refining.
Algorithms that efficiently distribute resources are becoming more and more important as technology develops.
Despite its tongue-in-cheek name, the Chocolate Distribution Problem is a prime example of the age-old quest to develop algorithms that strike a balance between elegance, efficiency, and precision when addressing difficult computational problems.

Conclusion:

The Chocolate Distribution Problem provides an interesting look into the complex world of algorithms and data structures. The path from the first brute-force method to the optimal solutions highlights the importance of algorithmic efficiency in solving problems. With the help of ideas like sorting and sliding windows, programmers can solve complex problems in the real world with style and accuracy.

We observe the balance between accuracy and efficiency as we work through the complexities of this issue. Although the brute-force approach yields an accurate result, its scalability is limited. While the sorting and sliding window methods increase productivity, they must be used carefully.

The ideal solution ultimately demonstrates the elegance of algorithmic design. It not only satisfies the time complexity requirements but also shows how well different strategies can be combined to produce an innovative and effective solution. With its delicate undertones, the Chocolate Distribution Problem is a monument to the art and science of algorithmic problem-solving in the rapidly developing field of computer science.

Next TopicFind out the person who got the ticket last problem in queue

← prev next →