Lowest Common Ancestor in a Binary Search Tree

Binary Search Tree

A binary search tree is a type of a binary tree where all the values smaller than any node are present in its left subtree, and all the values greater than it are present at the right subtree.

Problem statement

We are given the root node of the binary search tree and two integer values, n and m. Our task is to return the lowest common ancestor present of both the nodes in the binary search tree.

For example: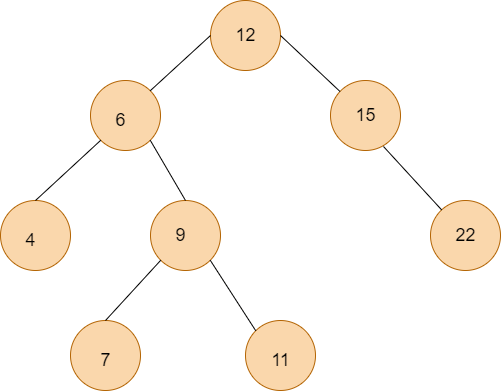

Lowest Common Ancestor in a Binary Search Tree

In the above example, we have a binary search tree, and we will find out the lowest common ancestors of some nodes.

n=6 and m=15, then the lowest common ancestor is 12
n=4 and m=22, then the lowest common ancestor is 12
n=7 and m=9, then the lowest common ancestor is 9

Approach 1

We will find out the root to node1 path and root to node2 path and store it into ArrayList. Now the first common element of the ArrayList will be the lowest common ancestor.

Java code:

import java.util.*;
public class Main {
//creating the node for the tree
    public static class Node{
        int data;
        Node left;
        Node right;
        Node(int data){
            this.data=data;
            this.left=null;
            this.right=null;
        }
    }
  public static void main(String[] args) {
        Node root= new Node(12);
        root.left=new Node(6);
        root.right=new Node(15);
        root.left.left=new Node(4);
        root.left.right=new Node(9);
        root.left.right.left=new Node(7);
        root.left.right.right=new Node(11);
        root.right.right=new Node(22);
        
        int node1 = 7;
        int node2 = 22;
        ArrayList<Integer> list1 = new ArrayList<>();
        ArrayList<Integer> list2 = new ArrayList<>();
        rootToNodePath(root,node1,list1);
        rootToNodePath(root,node2,list2);
        int p1=0;
        int p2=0;
        if(list1.size()>list2.size()){
            p1+=list1.size()-list2.size();
        }else{
            p2+=list2.size()-list1.size();
        }
        while(p1< list1.size() && p2<list2.size()){
            if(list1.get(p1)==list2.get(p2))
            break;
            p1++;
            p2++;
        }
        System.out.println("lowest common ancestor of node "+node1+" node "+node2+" is "+list1.get(p1));
  }
  public static void rootToNodePath(Node root,int node,ArrayList<Integer> list){
      list.add(0,root.data);
      if(root.data==node)
      return;
      if(root.data<node)
      rootToNodePath(root.right,node,list);
      else
      rootToNodePath(root.left,node,list);
  }
}

Output:

Time complexity: O(H)+O(H), where H is the height of the tree. In the worst case, it can be upto O(N).

Space complexity: O(N)+O(N) in the worst case.

Method 2

We will use recursion to get the lowest common ancestor of the nodes.

In the recursive call, if the current node is equal to node1 or node2, then the current node will be LCS.
If the value of the current node is lesser than a node and greater than the other node then the current node will be LCS.
If the value of the current node is lesser than the value of both the nodes then the answer will lie in the right subtree of the current node.
If the value of the current node is greater than the value of both the nodes, then the answer will lie in the left subtree of the current node.

Java code:

import java.util.*;
public class Main {
//creating the node for the tree
    public static class Node{
        int data;
        Node left;
        Node right;
        Node(int data){
            this.data=data;
            this.left=null;
            this.right=null;
        }
    }
  public static void main(String[] args) {
        Node root= new Node(12);
        root.left=new Node(6);
        root.right=new Node(15);
        root.left.left=new Node(4);
        root.left.right=new Node(9);
        root.left.right.left=new Node(7);
        root.left.right.right=new Node(11);
        root.right.right=new Node(22);
        
        int node1 = 4;
        int node2 = 11;
        int answer = getLowestCommonAncestor(root,node1,node2);
        System.out.println("lowest common ancestor of node "+node1+" node "+node2+" is "+answer);
  }
  public static int getLowestCommonAncestor(Node currentNode,int node1,int node2){
     if(currentNode.data==node1 || currentNode.data==node2){
         return currentNode.data;
     }
     
     if((currentNode.data<node1 && currentNode.data>node2)||(currentNode.data<node2 && currentNode.data>node1)){
         return currentNode.data;
     }
     
     if(currentNode.data<node1 && currentNode.data<node2){
         return getLowestCommonAncestor(currentNode.right,node1,node2);
     }
     
     if(currentNode.data>node1 && currentNode.data>node2){
         return getLowestCommonAncestor(currentNode.left,node1,node2);
     }
     return -1;
  }
}

Output:

Time complexity: O(N) in the worst case; otherwise, O(H) where H is the height.

Space complexity: O(H) auxiliary recursion space stack.

Method 3

This approach is the iterative approach of the above solution. It will help us to save the auxiliary stack space occupied by the recursion.

Java code:

import java.util.*;
public class Main {
//creating the node for the tree
    public static class Node{
        int data;
        Node left;
        Node right;
        Node(int data){
            this.data=data;
            this.left=null;
            this.right=null;
        }
    }
  public static void main(String[] args) {
        Node root= new Node(12);
        root.left=new Node(6);
        root.right=new Node(15);
        root.left.left=new Node(4);
        root.left.right=new Node(9);
        root.left.right.left=new Node(7);
        root.left.right.right=new Node(11);
        root.right.right=new Node(22);
        
        int node1 = 7;
        int node2 = 15;
        int answer=-1;
        Node currentNode = root;
        while(currentNode!=null){
            if(currentNode.data==node1 || currentNode.data==node2){
                 answer = currentNode.data;
                 break;
            }
            if((currentNode.data<node1 && currentNode.data>node2)||(currentNode.data<node2 && currentNode.data>node1)){
                 answer = currentNode.data;
                 break;
            }
            if(currentNode.data<node1 && currentNode.data<node2){
                currentNode=currentNode.right;
            }
            if(currentNode.data>node1 && currentNode.data>node2){
                currentNode=currentNode.left;
            }
        }
        System.out.println("lowest common ancestor of node "+node1+" node "+node2+"  is "+answer);
  }

}

Output: