Advantages of Threaded Binary Tree

A Binary Tree is a data structure that can be represented with the help of an Array or a Linked List. Whenever the representation of a Binary Tree is done using a Linked List, the nodes of the list are not stored at adjacent or neighboring memory addresses. They are linked to each other through the parent-child relationship associated with trees.

In this representation, every node consists of three different components:

1. A pointer pointing toward the Left Node,
2. A pointer pointing toward the Right Node, and
3. A Data Element.

If a node in a Binary Tree does not have a left or right child or is a leaf node, then the absence child node is denoted by a NULL pointer.

Let us consider the following Binary Tree as an example.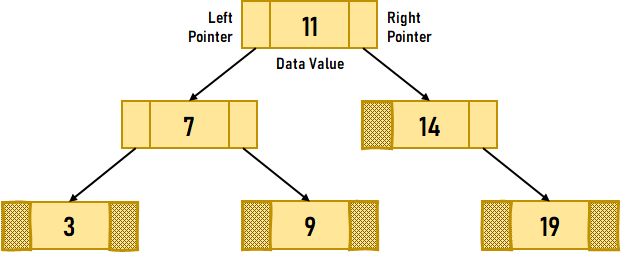

Figure 1. A Binary Tree

The above figure exemplifies that there are many nodes present in this that hold a NULL value in their Left or Right child pointer. We can use the space occupied by these NULL values in order to store some kind of valuable information.

One feasible way to use this space is to have a special pointer pointing to the nodes higher in the Tree (i.e., Ancestors). These special pointers are known as Threads, and the Binary Tree consisting of such pointers is known as the Threaded Binary Tree.

A Threaded Binary Tree is one of the variants of a normal Binary Tree that assists faster tree traversal and doesn't need a Stack or Recursion. It reduces memory wastage by placing the null pointers of a leaf node to the in-order successor or in-order predecessor.

In the following tutorial, we will learn about the advantages of the Threaded Binary Tree. But before we get started, let's briefly understand the Threaded Binary Tree and its types.

Understanding the Threaded Binary Tree

A Threaded Binary Tree is a Binary Tree where all left child pointers are NULL points to its in-order predecessor, and all right child pointers are NULL points to its in-order successor.

Moreover, the leftmost and the rightmost child pointer of a Treaded Binary Tree always points to null as their in-order predecessor and successor do not exist.

Let us consider the following example of a Threaded Binary Tree in order to understand the above statements.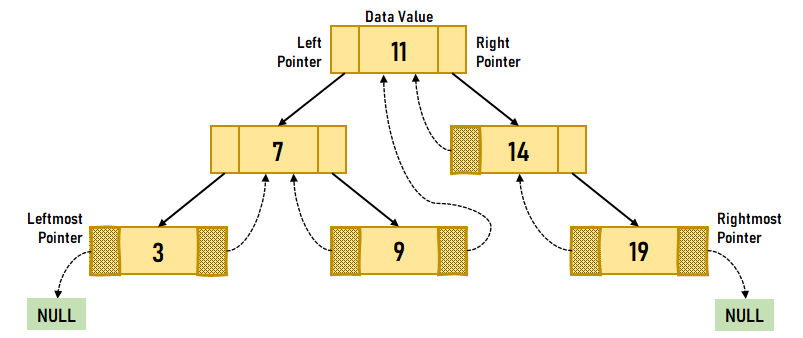

Figure 2. A Threaded Binary Tree

In the diagram shown above, we can observe that the right pointer of the node value 7 points to 9:

1. We will now check the left pointer of node 9, and if it is NULL, we will modify the address to the predecessor of the node, which is 7.
2. We will then check for the right pointer, and if it turns out to be NULL, we will modify the reference to the successor node, which is 11. Thus, it will point to 11.
3. We have used the threads (represented by the dotted lines) to point to the in-order predecessors/successors in Left/Right pointers, as shown in the figure above, and that's the reason why it is called a Threaded Binary Tree.
4. Moreover, the leftmost pointer of this tree, which is the left pointer of node value 3, and the rightmost pointer of the tree, which is the right pointer of node value 19, will point to NULL.

The primary objective of creating such as structure is to make the in-order and pre-order traversal of the binary tree faster without any help of additional data structure (like an auxiliary stack) or memory for its traversal.

Understanding the Types of Threaded Binary Tree

There are two types of Threaded Binary Trees:

1. Single Threaded Binary Tree
2. Double Threaded Binary Tree

Let us understand the types mentioned earlier in brief.

Single Threaded Binary Tree

The Single Threaded Binary Tree is a Threaded Binary Tee where only the right NULL pointers are made in order to point to the in-order successor.

Structure of a Node in Single Threaded Binary Trees:

The structure of a node in a Binary Threaded Tree is pretty much identical to that of a Binary Tree; however, with a few adjustments. In Threaded Binary Trees, we use additional Boolean variables in the node structure. We will only use a variable representing the right thread for the Single Threaded Binary Trees.

Let us consider the following snippet of code illustrating the structure of a node in C++ Language:

Syntax:

Let us now consider the following diagram depicting an example of a Single Threaded Binary Tree.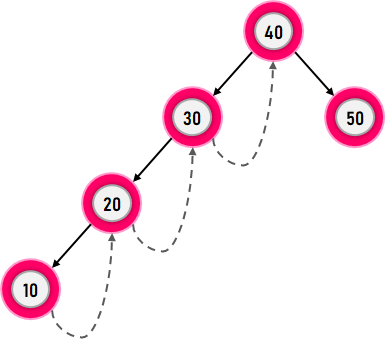

Figure 3. A Single Threaded Binary Tree

In the diagram shown above, we can observe that the node value 10 does not consist of any child nodes. So, the right pointer of node value 10 is null; therefore, it is pointing to its in-order successor, i.e., node value 20, through a thread. In the same way, the other nodes of this tree consisting of a right null pointer refer to their in-order successor, as depicted in the diagram.

Double Threaded Binary Tree

The Double Threaded Binary Tree is a Threaded Binary Tree where the left, as well as the right NULL pointers, are made in order to point towards the in-order predecessor and in-order successor, respectively. (Here, the left threads are supportable in the reverse in-order traversal of the tree.)
Structure of a Node in Double Threaded Binary Trees:

We will use two Boolean variables representing the left and right threads for the Double Threaded Binary Trees.

Let us consider the following snippet of code illustrating the structure of a node in C++ Language:

Syntax:

In the above snippet of code, the Boolean variables, left_thread, and right_thread, help us to differentiate whether the left/right pointer stores the in-order predecessor/successor or left/right child.

Let us now consider the following diagram depicting an example of a Single Threaded Binary Tree.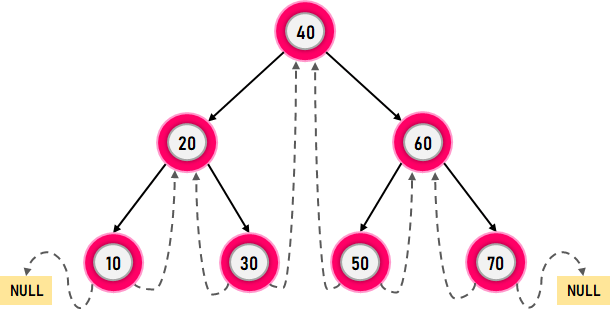

Figure 4. A Double Threaded Binary Tree

The above diagram is a representation of a Double Threaded Binary Tree. Here, we can observe that the node value 30 has no left and right child. Therefore, its left pointer points towards its in-order predecessor, i.e., node value 20, and its right pointer points towards its in-order successor, i.e., node value 40. In a similar way, the other nodes of this tree with a left/right null pointer refer to their in-order predecessor/successor with the help of the threads.

Understanding the Advantages of the Threaded Binary Tree

There are numerous advantages of a Threaded Binary Tree over a Non-Threaded Binary Tree. Some of them are listed below:

1. The first advantage of using a Threaded Binary Tree is that the traversal operation is much faster than that of the Non-Threaded Binary Tree, as the non-recursive implementation is possible with a Threaded Binary Tree which can execute faster and does not require the infliction of stack management.
2. The second advantage of using the Threaded Binary Tree is that we can efficiently determine the predecessor and successor nodes beginning from any node. However, this activity is much more time-consuming and tedious in the case of a Non-Threaded Binary Tree, as it uses the stack to provide upward-pointing information in the tree. The same can be done with the help of threads instead of using a stack mechanism in the Threaded Binary Tree.
3. Another advantage of a Threaded Binary Tree is that one can access any node from another. Threads are generally more upward, whereas the links are downward. Therefore, one can move in their direction in a threaded tree, and its nodes are circularly linked. This is impossible in Non-Threaded Binary Tree because we can only move in a downward direction beginning from the root.
4. Another advantage of using a Threaded Binary Tree is that it reduces memory waste. Whenever the left/right pointer of a normal Binary Tree is NULL, memory is wasted. However, one can overcome this problem with the help of the Threaded Binary Tree by storing its in-order predecessor/successor.
5. One can also perform a backward traversal using a Double-Threaded Binary Tree.
6. In-order Traversal in a Threaded Binary Tree is fast because we get the next node in O(1) time than a normal Binary Tree that takes O(height). However, the operations like insertion and deletions operations take more time in the case of a Threaded Binary Tree.

Understanding some Disadvantages of the Threaded Binary Tree

Let us now discuss some of the disadvantages of the Threaded Binary Tree:

1. The main disadvantage of a Threaded Binary Tree is its complicated insertion and deletion operations. These operations become more time-consuming, and their process is highly complex by storing the in-order predecessor/successor for the node with a null left/right pointer.
2. The additional memory is also used in the form of the variables defined for the left and right threads in order to distinguish between a thread from an ordinary link. (But there are more effective methods to differentiate between a thread and an ordinary link.)

The Conclusion

The above tutorial taught us about the Threaded Binary Tree and its types. We have also discussed various advantages of the Threaded Binary Tree along with some disadvantages.