TRANSITIONS OF MATRIX

Introduction

The transition of matrices making them in the realm of computational mathematics and matrix manipulation, the concept of changing the number of transitions to make two matrices equal, is a fascinating problem with different operations. This task involves determining the minimal number of operations needed to transfigure one matrix into another through a series of transitions.

Matrix transitions can encompass colorful operations such as switching rows or columns, modifying individual rudiments, or applying more complex metamorphoses. The idea is to optimize these operations to minimize the overall number of ways demanded for parity.

This problem isn't only applicable in the field of direct algebra but also holds significance in computer wisdom, image processing, and optimization algorithms. Understanding the minimal transitions needed to equate matrices is essential to effective algorithm design, data manipulation, and resource application.

In this discourse, we will claw into the strategies, algorithms, and fine principles that govern the hunt for the minimal number of transitions between matrices. Whether for practical operations or theoretical analysis, the pursuit of equivalency between matrices through minimum transitions presents a formidable challenge in the world of numerical calculation.

Given two matrices, A and B, of order n * m, the task is to find the needed number of metamorphoses so that both matrices are equal; print 1 if it isn't possible.

Transformation Steps:

The transformation steps are as follows:

• Elect any one matrix out of two matrices.
• Choose either row or column of the named matrix.
• Proliferation of every element of a select row or column by 1.

Reasons behind the result:

The crucial reasons behind the result of this problem are

• Incrementing any row of A () is the same as decrementing the same row of B ().
• So, we can have the result after having the metamorphosis on only one matrix, either incrementing or decrementing.
• For every metamorphosis, either the 1st row or the 1st column element inescapably changed; the same is true for the other i-th row or column.
• If(A(i)(j) - A(i)(0) - A(0)(j) A (0)(0)! = 0), then no result exists.
• The rudiments of the 1st row and 1st column only lead to a result.

Implementation:

Output:

The output of the above code is as follows: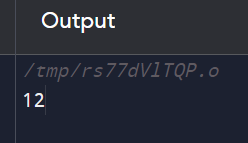

Explanation:

This C program is designed to find the minimal number of operations needed to make two matrices equal. The matrices involved are represented by arrays A and B, both having a maximum size of 1000x1000 (defined by m).

The main function, count Ops, takes four parameters: matrices A and B and their confines m and n. It first updates matrix A by abating the matching rudiments of matrix B. This is done to simplify the problem by reducing it to change the minimal number of operations to make A a zero matrix.

The program also checks a necessary condition for the actuality of a valid set of operations. It iterates over the matrices starting from indicator (1,1) and checks if the sum of the rudiments in the submatrix formed by the current element and the top row and left column (banning the common element) is equal to the element at (0,0). Still, the function returns 1, indicating that a valid set of operations isn't possible if this condition isn't met for any element.

Still, the program calculates the total number of operations demanded to make matrix A a zero matrix if the necessary condition is satisfied. The result is attained by casting the absolute values of the rudiments in the first column and the differences between the rudiments in the first row and the element at (0, 0). This is grounded in the observation that the values in the first row and column are determined by the element at (0,0) in a valid set of operations.

Eventually, the main function initializes two matrices, A and B, and calls the COS function within the confines of the matrices (3x3 in this case). The result is also published in print.

In the handed illustration, the matrices A and B aren't originally equal, and the program calculates and prints the minimal number of operations needed to make them equal.

Conclusion:

In conclusion, the hunt to determine the number of transitions demanded to make two matrices equal reveals a rich shade of fine challenges and algorithmic complications. This pursuit isn't simply an exercise in computational effectiveness but a trip through the core principles of direct algebra, optimization, and algorithm design.

Through our discourse, we have uncovered the significance of matrix parity in colorful fields, from computer wisdom to image processing. The significance lies not only in the theoretical understanding of matrix metamorphoses but also in the practical counteraccusations for algorithmic effectiveness and resource application.

As we navigate the geography of matrix equivalency, we encounter a myriad of strategies and algorithms, each offering a unique perspective on how to minimize transitions. These approaches reflect the interplay between fineness and computational pragmatism, illustrating the delicate balance needed to solve this complex problem.

The hunt for the minimal number of transitions is a testament to the beauty and depth of fine problem-solving. It challenges us to think critically, explore different pathways, and apply innovative ways to optimize the metamorphosis process. As we conclude our discourse, the trip to equivalency between matrices not only enhances our understanding of abecedarian fine generalities but also paves the way for more effective computational results in a variety of real-world operations.