Find the Index of the Number Using a Binary Tree

Finding out the index of a number within a binary tree is a common task and involves references to its left and right child. The term index in the node typically refers to a position of a node within the tree that allows for efficient navigation and access to specified nodes. The binary tree doesn't have the straightforward concept of the index; rather, they have a structured way in which each nod comprises the left and right node, and then each node narrows down to a leaf node.

Some advantages of the index in the binary tree are: -

Indices help in the efficient search and various other searching techniques in the binary tree.
It also provides flexibility when it comes to insertion operation, deletion, or we have to make any changes in the node.
They are also helpful in handling extensive datasheets due to their logarithmic time complexities.
They are also compatible with a variety of different trees such as AVL tree, Red-black Tree, and several others. They can be very beneficial in the storage management process.

In this article, we will explore the concept of finding the index of a binary tree and see the program for the same in different programming languages.

Implementation

// Writing a C++ program to find out the index of the binary tree 
#include <iostream>

using namespace std;

//First, we have to return the sum of the array with the index of 0, and this function tells us that the array has already been made. The sum of the element stored in the array is already present in the binary search tree.
int getSum(int BTree[], int ind_x)
{
	int sum = 0; // Initialize result

	//The index in a binary tree is usually one more than the index in the array.
	ind_x = ind_x + 1;

	//Explore or traverse the ancestors 
	while (ind_x>0)
	{
		//Now, we have to add the current element of the tree to the sum function
		sum += BTree[ind_x];

		// next, we have to move the index to the parent node
		ind_x -= ind_x & (-ind_x);
	}
	return sum;
}

void updateBIT(int BTree[], int n, int ind_x, int val)
{
	// index of the binary tree is one more than the index in the array
	ind_x = ind_x + 1;

	//We have to visit all the ancestors
	while (ind_x <= n)
	{
	//Now, we have to add value to the current node of the tree
	BTree[ind_x] += val;

	//We have to update the index of the parent node
	ind_x += ind_x & (-ind_x);
	}
}

// We have to build a binary indexed tree with the array of size n 
int *constructBTree(int arr[], int n)
{
	//Now, we have to create and initialize a binary tree of size 0
	int *BTree = new int[n+1];
	for (int i=1; i<=n; i++)
		BTree[i] = 0;

	// Now, we have to store the actual values of the binary tree by using the update function
	for (int i=0; i<n; i++)
		updateBIT(BTree, n, i, arr[i]);

	//We have to uncomment all the lines stated below to see the contents of the binary tree
	//for (int i=1; i<=n; i++)
	//	 cout << BTree[i] << " ";

	return BTree;
}


// writing the main program to test the above functions
int main()
{
	int freq[] = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9};
	int n = sizeof(freq)/sizeof(freq[0]);
	int *BTree = constructBTree(freq, n);
	cout << "Sum of elements in arr[0..5] is "
		<< getSum(BTree, 5);

	freq[3] += 6;
	updateBIT(BTree, n, 3, 6); //Update BIT for above change in arr[]

	cout << "\nSum of elements in arr[0..5] after update is "
		<< getSum(BTree, 5);

	return 0;
}

Output:

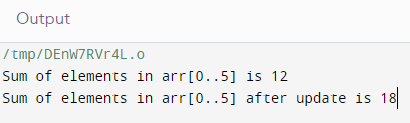
Find the Index of the Number Using a Binary Tree

A step-by-step introduction to the code

The code begins by including all the necessary headers of the files for carrying out the various input and output operations.
Next, we define a 'getSum' function which is responsible for getting the sum and has two parameters, one is BSTree, and the other one is Ind, which is an index.
Inside the 'getSum' function, we initialize the value to 0 so that it will store the value of the sum.
The 'index' in the BITree will be increased by 1.
Next, we must create a while loop and traverse all the ancestors of the currently present node.
Inside the loop, the current element of the binary tree is added to the sum.
Next, we have to modify the index to the parent node, and we will do that by subtracting the most specific bit.
After that, we finally get the sum back as 0.
We then create the 'updateBSTree' function, which will update the index in the binary tree.
As we saw in the 'getSum' function, the index is incremented by 1 to get matched indexing for the BSTree.
Then we create a while loop to traverse all the indexes of the BST.
Inside the loop, the value of the present node is added to the BSTree.
The primary function of the program serves as the entry point of the program and is used to test the above functions.
The 'getSum' function obtains the sum of the elements in the binary tree, and BSTree is generally taken up as the argument, and the result is printed accordingly.

Example 2)

// Writing a Java program to find out the index of the binary tree 
import java.util.*;
import java.lang.*;
import java.io.*;

class BinaryInd_xedTree
{
	// stating the maximum size of the tree
	final static int MAX = 1000;	

	static int BTree[] = new int[MAX];
// First, we have to return the sum of the array with the index of 0, and this function tells us that the array has already been made; the sum of the element stored in the array are already present in the binary search tree.
	int getSum(int ind_x)
	{
		int sum = 0; // Initialize result
	
	//The index in a binary tree is usually one more than the index in an array.
		ind_x = ind_x + 1;
	//Explore or traverse the ancestors 
		while(ind_x>0)
		{
		//Now, we have to add the current element of the tree to the sum function
			sum += BTree[ind_x];
		// next, we have to move the index to the parent node
			ind_x -= ind_x & (-ind_x);
		}
		return sum;
	}
	public static void updateBIT(int n, int ind_x,
										int val)
	{
	// index of the binary tree is one more than the index in array
		ind_x = ind_x + 1;
	//We have to visit all the ancestors
		while(ind_x <= n)
		{
	//Now, we have to add value to the current node of the tree
		BTree[ind_x] += val;
	//We have to update the index of the parent node
		ind_x += ind_x & (-ind_x);
		}
	}

// We have to build a binary indexed tree with the array of size n 
	void constructBTree(int arr[], int n)
	{
	//Now, we have to create and initialize a binary tree of size 0
		for(int i=1; i<=n; i++)
			BTree[i] = 0;
	
	// Now, we have to store the actual values of the binary tree by using the update function
		for(int i = 0; i < n; i++)
			updateBIT(n, i, arr[i]);
	}

// writing the main program to test the above functions
	public static void main(String args[])
	{
		int freq[] = {2, 1, 1, 3, 2, 3,
					4, 5, 6, 7, 8, 9};
		int n = freq.length;
		BinaryInd_xedTree tree = new BinaryInd_xedTree();

		tree.constructBTree(freq, n);

		System.out.println("Sum of elements in arr[0..5]"+
						" is "+ tree.getSum(5));
		updateBIT(n, 3, 6);

		//We have to find the sum after the value is changed
		System.out.println("Sum of elements in arr[0..5]"+
					" after update is " + tree.getSum(5));
	}
}

Output:

A step-by-step introduction to the code

The code begins by importing the necessary Java packages for the program.
Next, we define a 'getSum' function which is responsible for getting the sum and has two parameters, one is BSTree, and the other one is Ind, which is an index.
Inside the 'getSum' function, we initialize the value to 0 so that it will store the value of the sum.
The 'index' in the BITree will be increased by 1.
Next, we have to create a while loop and traverse all the ancestors of the currently present node.
Inside the loop, the current element of the binary tree is added to the sum.
Next, we have to modify the index to the parent node, and we will do that by subtracting the most specific bit.
After that, we finally get the sum back as 0.
We then create the 'updateBSTree' function, which will update the index in the binary tree.
As we saw in the 'getSum' function, the index is incremented by 1 to get matched indexing for the BSTree.
Then we create a while loop to traverse all the indexes of the BST.
Inside the loop, the value of the present node is added to the BSTree.
The primary function of the program serves as the entry point of the program and is used to test the above functions.
The 'getSum' function obtains the sum of the elements in the binary tree, and BSTree is generally taken up as the argument, and the result is printed accordingly.