Palindrome substring queries

Given a string and a list of queries which specifies ranges both inclusive and need to find whether the substring in the specified range is a palindrome or not

Consider a scenario where we have an input string "abaaabaaaba" and a set of queries: [0, 10], [5, 8], [2, 5], [5, 9]. Our task is to determine whether the substrings specified by these query indices are palindromes or not.

For instance:

To address Q such queries for an input string of length N, there are two main approaches:

Method 1 (Naive Approach):

In this method, we iterate through each query individually and examine whether the specified substring is a palindrome. Since there are Q such queries, and each query can take O(N) as the worst-case time to determine palindromes, this approach has a worst-case time complexity of O(Q* N). While this method is space-efficient, there exists a more efficient alternative.

Java implementation of the approach

Output: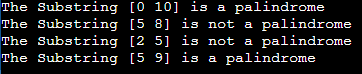

Time Complexity:

Checking each substring for palindrome properties involves comparing characters from the left and right.

For each query with a substring of length N, the time complexity is O(N).

If there are Q queries in total, the overall time complexity is O(Q * N), where Q is the number of queries in the question given and N is the maximum length of the substrings.

Space Complexity:

The space complexity is O(1) because the amount of additional memory used by the program does not depend on the input size. It only uses constant memory for variables and data structures regardless of the input string length or the number of queries.

Method 2 (Cumulative Hash):

The concept behind this approach is analogous to the Rabin-Karp string-matching algorithm. It relies on string hashing and involves calculating cumulative hash values for the original and reversed strings, storing them in two arrays: prefix[] and suffix[].

Overflow Issues:

Hash values can become extremely large, even for small strings.

To avoid overflows, the code performs all operations modulo 1000000007, a prime number chosen for mathematical reasons. This prime fits within an integer value.

Java and Python can handle these large values without modulo operations.

The key modulo operations used in the program are:

Addition: (a + b) % M = (a % M + b % M) % M

Multiplication: (a * b) % M = (a * b) % M

Mixture of addition and multiplication: (a * x + b * y + c) % M = ((a * x) % M + (b * y) % M + c % M) % M

Subtraction: (a - b) % M = (a % M - b % M + M) % M

Division: (a / b) % M = (a * MMI(b)) % M, where MMI() calculates the Modulo Multiplicative Inverse, implemented by the findMMI() function in the program.

Java Implementation

Output: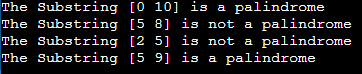

Working:

Input:

String: "abbaaba"

Queries: [0, 6], [1, 4], [2, 5], [0, 3]

Step 1: Constants and Helper Functions

BASE is set to 101.

MODULO is set to 1000000007.

Step 2: Precompute Powers of BASE

We precompute an array of powers of BASE for efficient hashing. For this example, let's assume powersOfBase is [1, 101, 101^2, ..., 101^6].

Step 3: Compute Prefix and Suffix Hashes

We compute two arrays:

prefixHash: Stores hash values for the original string "abbaaba."

suffixHash: Stores hash values for the reversed string "abaabba."

Let's assume these arrays are filled as follows:

prefixHash: [0, 97, 10098, ..., HashValueAtIndexN]

suffixHash: [0, 97, 10098, ..., HashValueAtIndexN]

These arrays are computed using modular arithmetic and the powers of BASE.

Step 4: Process Queries

We have four queries, and we want to determine if the specified substrings are palindromes.

Query 1: [0, 6]

Calculate hash values for the substring "abbaaba" using prefixHash and powersOfBase.

Calculate hash values for the reversed substring "abaabba" using suffixHash and powersOfBase.

Compare the hash values. If they match, compare characters using isPalindrome. In this case, they match, so it's a palindrome.

Query 2: [1, 4]

Calculate hash values for the substring "bbaa" using prefixHash and powersOfBase.

Calculate hash values for the reversed substring "aabb" using suffixHash and powersOfBase.

Compare the hash values. They don't match, so it's not a palindrome.

Query 3: [2, 5]

Similar to Query 2, calculate hash values for the substring "baab" and its reverse.

Again, the hash values don't match, so it's not a palindrome.

Query 4: [0, 3]

Calculate hash values for the substring "abba" using prefixHash and powersOfBase.

Calculate hash values for the reversed substring "abba" using suffixHash and powersOfBase.

The hash values match, and isPalindrome confirms that it's a palindrome.

Time Complexity: O(n*m)

Space Complexity: O(n)