Bitonic Sort Algorithm

In this article, we will discuss the Bitonic sort Algorithm. Bitonic sort is a parallel sorting algorithm that performs O(n²log n) comparisons. Although the number of comparisons is more than that in any other popular sorting algorithm, it performs better for the parallel implementation because elements are compared in a predefined sequence that must not depend upon the data being sorted. The predefined sequence is called the Bitonic sequence.

To understand the bitonic sort, we first have to understand the Bitonic sequence.

In Bitonic sequence, elements are first arranged in increasing order, and then after some particular index, they start decreasing.

An array with A[0…i…n-1] is said to be bitonic, if there is an index i, such that -

Where, 0 ≤ i ≤ n-1.

Before moving directly towards the algorithm of bitonic sort, first, understand the conversion of any random sequence into a bitonic sequence.

How to convert the random sequence into a bitonic sequence?

Consider a sequence A[ 0 ... n-1] of n elements. First, start constructing a Bitonic sequence by using 4 elements of the sequence. Sort the first 2 elements in ascending order and the last 2 elements in descending order, concatenate this pair to form a Bitonic sequence of 4 elements. Repeat this process for the remaining pairs of the element until we find a Bitonic sequence.

Let's understand the process to convert the random sequence into a bitonic sequence using an example.

Suppose the elements of array are - {30, 70, 40, 80, 60, 20, 10, 50}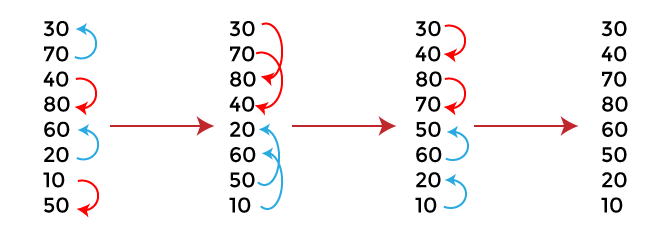

After conversion, the bitonic sequence that we will get is -

30, 40, 70, 80, 60, 50, 20, 10

Now, move towards the steps of performing the bitonic sort.

Steps to perform Bitonic sort

The steps used to perform the bitonic sort are listed as follows -

1. In first step, we have to create the bitonic sequence from the given random sequence as we have done above. It is considered as the first step of the process. After this step, we will get a sequence in which the elements in the first half are arranged in ascending order, while the elements of the second half are arranged in descending order.
2. Now, in the second step, we have to compare the first element of first half with the first element of second half, then second element of first half with the second element of second half, and so on. Here, we have to swap the elements if any element in the second half is found to be smaller.
3. After the above step, we got all the elements in the first half smaller than all the elements in the second half. The compare and swap results into the two sequences of n/2 length each. Repeat the process performed in the second step recursively onto every sequence until we get a single sorted sequence of length n.

Now, let's see the entire procedure of bitonic sort with an example. It will be easier to understand the bitonic sort with an example as it makes the explanation clearer and easier.

In the below example, we are using the bitonic sequence given above that we created from a random sequence.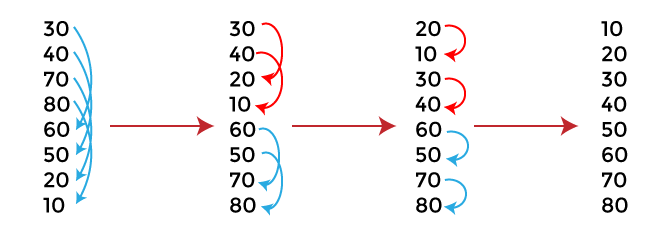

Now, the given array is completely sorted.

Bitonic sort complexity

Now, let's see the time complexity of bitonic sort in the best case, average case, and worst case. We will also see the space complexity of bitonic sort.

1. Time Complexity

The time complexity of bitonic sort is O(log² n) in all three cases.

2. Space Complexity

• The space complexity of bitonic sort is O(n log²n).

Implementation of Bitonic sort

Now, let's see the programs of Bitonic sort in different programming languages.

Program: Write a program to implement bitonic sort in C language.

Output

After the execution of the above code, the output will be -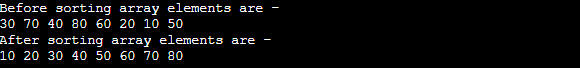

Program: Write a program to implement bitonic sort in C++.

Output

After the execution of the above code, the output will be -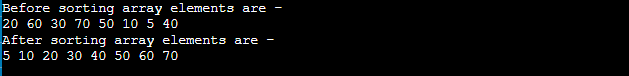

Program: Write a program to implement bitonic sort in C#.

Output

After the execution of the above code, the output will be -

Program: Write a program to implement bitonic sort in Java.

Output

After the execution of the above code, the output will be -

So, that's all about the article. Hope the article will be helpful and informative to you.